扬州网络科技有限公司网站建设seo交流群
中值滤波
文章目录
- 中值滤波
- 理解中值滤波的过程
- Matlab 实现
- 实际应用
- 频域分析
中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序,然后使用中间值作为输出。
中值滤波的数学公式如下:
y[n]=median(x[n−k],…,x[n],…,x[n+k])y[n]=\operatorname{median}(x[n-k],\dots,x[n],\dots,x[n+k])y[n]=median(x[n−k],…,x[n],…,x[n+k])
其中 xxx 是原始信号,yyy 是滤波后的信号,nnn 是当前位置,kkk 是窗口大小。
理解中值滤波的过程
为了更好地理解中值滤波的过程,我们可以使用一个简单的数组。假设我们有一个长度为 7 的数组 xxx,如下所示:
x = [1, 3, 2, 4, 6, 5, 7]
现在,我们想对这个数组进行中值滤波,窗口大小为 3。首先,我们需要将窗口移动到数组的第一个元素:
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 窗口最后一个元素| 窗口中间的元素窗口第一个元素
然后,我们需要将窗口内的元素排序:
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 排序后的窗口最后一个元素| 排序后的窗口中间的元素排序后的窗口第一个元素
排序后,我们可以使用排序后的窗口的中间值作为输出。在这个例子中,中间的值是 3,因此输出为 3。
接下来,我们将窗口向右移动一个元素,并重复这个过程,直到处理完整个数组。
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 2| 3,2,41,2,3
经过中值滤波后,结果为:
y = [1, 2, 3, 4, 5, 5, 7]
Matlab 实现
下面是一个简单的 Matlab 实现,使用了 medfilt1 函数:
% 生成一个随机信号
x = [1, 3, 2, 4, 6, 5, 7];% 中值滤波
y = medfilt1(x, 3);
在这个例子中,我们生成了一个长度为 7 的数组,并使用了 medfilt1 函数对数组进行了中值滤波,窗口大小为 3。
y 的输出结果为 [1, 2, 3, 4, 5, 5, 7]。
实际应用
中值滤波广泛应用于信号处理领域,特别是在声音和图像处理中。在声音处理中,中值滤波可以去除录音中的杂音和爆裂声。在图像处理中,中值滤波可以去除图像中的椒盐噪声和斑点噪声。
好的,这里是一个基于虚拟的音频信号的 Matlab 代码例子,演示中值滤波去除噪声的效果,并绘制处理前后的图像进行对比:
% 生成一个包含噪声的虚拟音频信号
Fs = 44100; % 采样频率
t = 0:1/Fs:5; % 时间范围
f1 = 1000; % 基频
f2 = 4000; % 频率偏移量
x = sin(2*pi*f1*t) + sin(2*pi*(f1+f2*t).*t) + 0.1*randn(size(t));% 绘制原始音频信号的时域图和频谱图
subplot(2,2,1)
plot(t,x)
title('原始信号的时域图')
xlabel('时间 (s)')
ylabel('幅值')
subplot(2,2,2)
f = linspace(0,Fs,length(x));
X = fft(x);
plot(f,abs(X))
title('原始信号的频谱图')
xlabel('频率 (Hz)')
ylabel('幅值')% 对音频信号进行中值滤波处理
win_size = 101;
y = medfilt1(x, win_size);% 绘制处理后的音频信号的时域图和频谱图
subplot(2,2,3)
plot(t,y)
title('处理后的信号的时域图')
xlabel('时间 (s)')
ylabel('幅值')
subplot(2,2,4)
Y = fft(y);
plot(f,abs(Y))
title('处理后的信号的频谱图')
xlabel('频率 (Hz)')
ylabel('幅值')
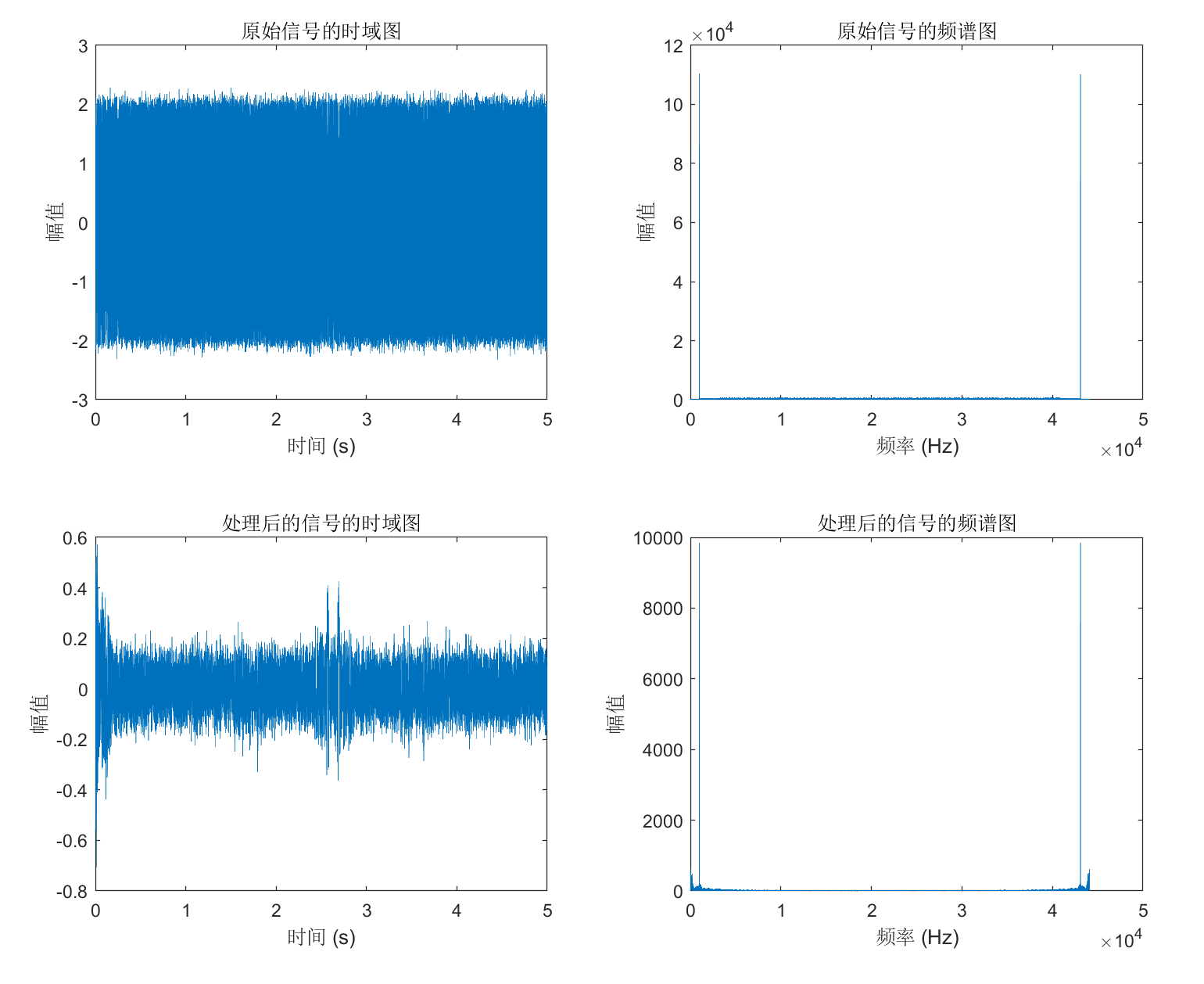
在这个例子中,我们首先生成了一个包含噪声的虚拟音频信号,然后使用 medfilt1 函数对其进行中值滤波处理。接下来,我们绘制了原始音频信号和处理后的音频信号的时域图和频谱图,可以看到,处理后的音频信号的噪声明显减少,幅值更加平滑。
频域分析
从微分方程的角度出发,可以将中值滤波看作是一个差分方程,进而分析其幅频响应。对于一个窗口大小为 3 的中值滤波,其差分方程为:
y[n]=median(x[n−1],x[n],x[n+1])y[n] = \operatorname{median}(x[n-1],x[n],x[n+1])y[n]=median(x[n−1],x[n],x[n+1])
可以将其转化为一个差分方程:
y[n]=12x[n]+14(x[n−1]+x[n+1])y[n] = \frac{1}{2} x[n] + \frac{1}{4} (x[n-1] + x[n+1])y[n]=21x[n]+41(x[n−1]+x[n+1])
其中,x[n]x[n]x[n] 是原始信号,y[n]y[n]y[n] 是滤波后的信号,nnn 是当前位置。
通过对差分方程进行离散化,可以得到其频域响应:
H(ejω)=12+14(e−jω+ejω)H(e^{j\omega}) = \frac{1}{2} + \frac{1}{4} (e^{-j\omega} + e^{j\omega})H(ejω)=21+41(e−jω+ejω)
H(ejω)=12+12cos(ω)H(e^{j\omega}) = \frac{1}{2} + \frac{1}{2} \cos(\omega)H(ejω)=21+21cos(ω)
因此,中值滤波的幅频响应为:
∣H(ejω)∣=(12+12cos(ω))2|H(e^{j\omega})| = \sqrt{\left(\frac{1}{2} + \frac{1}{2} \cos(\omega)\right)^2}∣H(ejω)∣=(21+21cos(ω))2
∣H(ejω)∣=12+12cos(ω)|H(e^{j\omega})| = \frac{1}{2} + \frac{1}{2} \cos(\omega)∣H(ejω)∣=21+21cos(ω)
下面是一个简单的 Matlab 实现,绘制了窗口大小为 3 的中值滤波的幅频响应曲线:
% 绘制窗口大小为 3 的中值滤波的幅频响应曲线
freq = linspace(0, pi, 1000);
H = 0.5 + 0.5*cos(freq);
plot(freq, H)
title('中值滤波的幅频响应')
xlabel('角频率 (rad)')
ylabel('幅值')
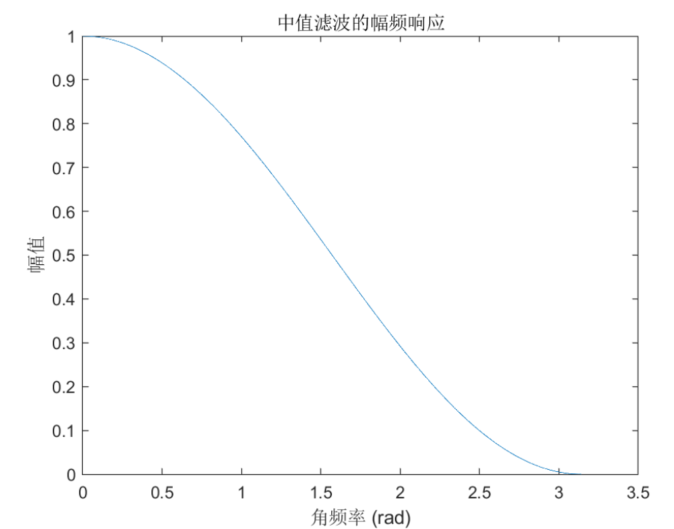
在这个例子中,我们使用 linspace 函数生成了一个包含 1000 个点的频率向量,然后使用中值滤波的幅频响应公式计算了每个点的幅值,并使用 plot 函数绘制了幅频响应曲线。
