门户类网站如何做策划永久免费linux服务器

一、矩阵乘法

从中可以看出，计算两个矩阵的乘积，需要三个 for 循环，可以简单写出代码：

	for(int i=1;i<=m;i++)for(int j=1;j<=p;j++)for(int k=1;k<=n;k++)c[i][j]+=a[i][k]*b[k][j];

时间复杂度的分析：很明显，三层for循环迭代，复杂度为  

二、Straasen 算法 

与简单的矩阵乘法计算不同，Strassen算法通过分治操作将运行变快，时间复杂度为 

1.Strassen 算法的原理：

        

 

简单的计算备用矩阵和式 ：通过简单的两层for循环将其加减

备用的乘积： 递归调用strassen算法，因为已逐步构造好分块的A和S矩阵，将需要的矩阵作为strassen的输入，就可以得出P矩阵

最后计算将C矩阵的四个分矩阵求出，再合并求得最后的C矩阵

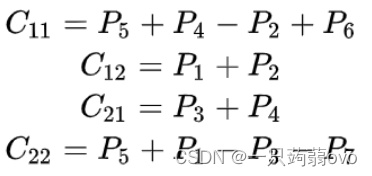
 ①矩阵相加减：

void plus(int **matrixa,int **matrixb,int **matrixc, int x) // 矩阵相加 
{for(int i=1;i<=x;i++)for(int j=1;j<=x;j++)matrixc[i][j]=matrixa[i][j]+matrixb[i][j];
}
void cut(int **matrixa,int **matrixb,int **matrixc,int x1) // 矩阵相减 
{for(int i=1;i<=x1;i++)for(int j=1;j<=x1;j++)matrixc[i][j]=matrixa[i][j]-matrixb[i][j];
}

② 矩阵的拆分（将一个矩阵分成四个小矩阵）与合并：

for(int i=1;i<=newx;i++)
for(int j=1;j<=newx;j++)
{                              a11[i][j]=ma[i][j];a12[i][j]=ma[i][j+newx];a21[i][j]=ma[i+newx][j];a22[i][j]=ma[i+newx][j+newx];b11[i][j]=mb[i][j];b12[i][j]=mb[i][j+newx];b21[i][j]=mb[i+newx][j];b22[i][j]=mb[i+newx][j+newx];
}for(int i=1;i<=newx;i++)
for(int j=1;j<=newx;j++) 
{mc[i][j]=c11[i][j]; mc[i][j+newx]=c12[i][j];mc[i+newx][j]=c21[i][j];mc[i+newx][j+newx]=c22[i][j];
}

 ③递归调用过程：

strassen(a11,s1,p1,newx);
strassen(s2,b22,p2,newx);
strassen(s3,b11,p3,newx);
strassen(a22,s4,p4,newx);
strassen(s5,s6,p5,newx);
strassen(s7,s8,p6,newx);
strassen(s9,s10,p7,newx);

 2.关于Strassen算法的理解：

        Strassen算法的理论推导是比较难的，或者说，是前人不断的试验发现得出的结果，因此需根据得出的公式打出代码。

        代码的难度在于很多地方。

        ①递归的调用：将预处理的代码通过递归计算出。        

        ②二维矩阵的存储以及二维数组在函数中的传递调用：

        因为在递归中的数组是反复调用的，所以一定不能使用全局数组导致计算混乱。

        另一个是二维矩阵的定义，不能简单定义静态数组，定义静态数组过大程序无法运行，并且运行速度慢，而应当定义malloc动态数组，数组大小可以改变，而且运行时高效很多。

malloc定义二维动态数组：

c=(int **)malloc(sizeof(int *)*n);
for(int i=1;i<=n;i++)c[i]=(int *)malloc(sizeof(int)*n);

三、Strassen 算法的改进

通过上述的理解，可以知道Straasen算法适用于当阶数为 2的幂（或者2的倍数） 时，是否能使其扩大适用范围，让任何相同阶数的矩阵算法都能使用。

当矩阵的阶数为奇数时，只需要将其行列各增加1，并且增加的元素全为0，即可使用 Straasen算法。

改进Strassen算法的复杂度：改进算法并未与原算法发生实质性的改变，因此时间复杂度不发生改变。