在STL的源代码中，map和set的底层原理都是红黑树。但这颗红黑树跟我们单独写的红黑树不一样，它需要改造一下：

改造红黑树

节点的定义

因为map和set的底层都是红黑树。而且map是拥有键值对pair<K,V>的，而set是没有键值对，只有一个K。因此，为了应对这两种不同的情况，就使用模板参数T。

当map使用这棵红黑树的时候，T就会变成pair<K,V>。当set使用时，T就会变成K。

//使用枚举
enum Colour
{RED,BLACK,
};// 如果是map，则为pair<K, V>; 如果是set，则为k
//因此，对于节点来说，需要再套一层模板，来应付两种不同的情况
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED)  //默认是红色{}
};

改版的红黑树的插入操作

红黑树的模板参数有三个：K、valueType和仿函数KeyOfValue。

K是key的类型，ValueTyp要么是set的K，要么是map的pair<const K,V>。

而仿函数是为了比较节点的值的大小的，因为官方库中键值对pair<K,V>比较大小的方法是比较first和second。但是红黑树中，新增节点是通过比较first，因此我们需要自己写一个仿函数用于单独比较first。

//跟节点的定义一样
//因为关联式容器中存储的是<key, value>的键值对，因此
// k为key的类型，
// ValueType: 如果是map，则为pair<K, V>; 如果是set，则为k。如下：
// map->RBTree<K,pair<const K,V>,MapKeyOfT> _t;
// set->RBTree<K,K,SetKeyOfT> _t
// 
// KeyOfValue: 通过value来获取key的一个仿函数类。其作用就是用于比较。
template<class K,class ValueType,class KeyOfValue>
class RBTree
{typedef RBTreeNode<ValueType> Node;
public: //迭代器typedef __RBTreeIterator<ValueType> iterator;//......
private:Node* _root = nullptr;
};

迭代器

红黑树的迭代器不能使用原生指针，因为它是一棵树，节点地址不连续，因此需要封装起来。

//set的K，map的pair<K,V>
template<class ValueType>
struct __RBTreeIterator
{typedef RBTreeNode<ValueType> Node;typedef __RBTreeIterator<ValueType> Self;Node* _node;__RBTreeIterator(Node* node):_node(node){}
};

1.operator++()

红黑树是二叉搜索树，采用的是中序遍历的方法。因此，迭代器每次向前走，是按照中序遍历的顺序走的。

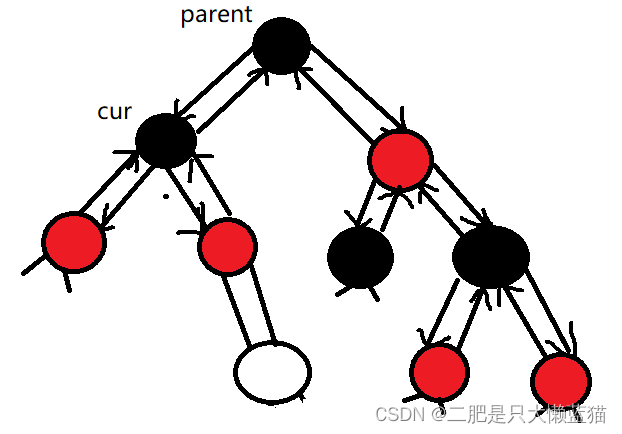
因此，对于往前++，有两种情况：第一种情况是当前节点的右孩子不为空，那么按照中序遍历的顺序，下一个节点便是右子树的最小值。第二种情况是当前节点的右孩子为空：这种情况下，又分两种情况：①当前节点是父节点的左孩子，那么下一个节点肯定是当前节点的父节点。②当前节点是父节点的右孩子，这意味着当前节点的父节点也被遍历了，又没有右孩子节点，只能往上找了，找的节点是祖先节点，而这个祖先节点是特征是：孩子节点是它的左节点。

 

	//左 根  右Self& operator++(){//当当前节点的右子树不为空，根据中序遍历的顺序，那就找右子树最小值if (_node->_right){Node* minValue = _node->_right;while (minValue->_left){minValue = minValue->_left;}//找到最小值的节点后，更新节点_node = minValue;}else  //当当前节的的右子树为空，说明它是叶子节点。此时需要判断情况{//判断当前节点是父亲节点的左孩子还是右孩子//第一种情况：如果是cur==parent->_right，即当前节点是父节点的右孩子的话，就//去找祖先节点（这个祖先节点的特征：孩子节点是它的左节点）//第二种情况：当前节点是父亲节点的左孩子，那么下一个节点就是父亲节点了Node* cur = _node;//定义父亲节点。Node* parent = cur->_parent;//如果当前节点不是父亲的右孩子，并且父亲是不存在，那么就是根节点或者是左孩子节点了//那就不进入循环。while (parent && cur == parent->_right){//如果是，那就往上找到下一个节点。cur = cur->_parent;parent = parent->_parent;}//更新节点_node = parent;}return *this;}

2.begin()和end();

迭代器的begin和end，是左闭右开的区间。那么begin就是最左的节点，end则是最右节点的下一个节点。这里不使用哨兵来作为end节点。

对于begin，就找到最左的节点就好啦！

iterator begin(){Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);}

对于end，这里选择直接置为空，传入匿名对象。这样子做的话，当遍历到最后一个节点后，它会往回遍历，一直到了根节点的上面一个节点，也就是空。此时就会结束循环。

	iterator end(){return iterator(nullptr);}

迭代器整体代码：

template<class ValueType>
struct __RBTreeIterator
{typedef RBTreeNode<ValueType> Node;typedef __RBTreeIterator<ValueType> Self;Node* _node;__RBTreeIterator(Node* node):_node(node){}ValueType& operator*(){return _node->_data;}ValueType* operator->(){return &_node->_data;}Self& operator++(){if (_node->_right){Node* minValue = _node->_right;while (minValue->_left){minValue = minValue->_left;}_node = minValue;}else {Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s){return _node != s._node;}
};

set的模拟实现

仿函数

由于set只有Key，因此就让仿函数直接返回Key值就可以了。

template<class K>class set{//set的仿函数，返回set的K值struct SetKeyOfValue{const K& operator()(const K& key){return key;}};

整体都是复用了红黑树的接口，并没有什么技术含量，问题都在红黑树中解决了。

namespace my_set
{template<class K>class set{//set的仿函数，返回set的K值struct SetKeyOfValue{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, K, SetKeyOfValue>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}bool insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfValue> _t;};

map的模拟实现：

仿函数

由于比较的是first，因此我们返回键值对中的first即可。

template<class K, class V>class map{struct MapKeyOfValue{const K& operator()(const pair<const K, V>& kv){return kv.first;}};

整体代码，一样的都是复用了红黑树的接口，并没有什么技术含量：

namespace my_map
{template<class K, class V>class map{struct MapKeyOfValue{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfValue>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}bool insert(const pair<const K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfValue> _t;};

最后是红黑树的整体代码，这段代码跟单独写的红黑树的代码差不多，就是在新增节点的操作那里，比较节点的值使用的是仿函数。

#pragma once//使用枚举
enum Colour
{RED,BLACK,
};// 如果是map，则为pair<K, V>; 如果是set，则为k
//因此，对于节点来说，需要再套一层模板，来应付两种不同的情况
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED)  //默认是红色{}
};template<class ValueType>
struct __RBTreeIterator
{typedef RBTreeNode<ValueType> Node;typedef __RBTreeIterator<ValueType> Self;Node* _node;__RBTreeIterator(Node* node):_node(node){}ValueType& operator*(){return _node->_data;}ValueType* operator->(){return &_node->_data;}//左 根  右Self& operator++(){//当当前节点的右子树不为空，根据中序遍历的顺序，那就找右子树最小值if (_node->_right){Node* minValue = _node->_right;while (minValue->_left){minValue = minValue->_left;}//找到最小值的节点后，更新节点_node = minValue;}else  //当当前节的的右子树为空，说明它是叶子节点。此时需要判断情况{//判断当前节点是父亲节点的左孩子还是右孩子//第一种情况：如果是cur==parent->_right，即当前节点是父节点的右孩子的话，就//去找祖先节点（这个祖先节点的特征：孩子节点是它的左节点）//第二种情况：当前节点是父亲节点的左孩子，那么下一个节点就是父亲节点了Node* cur = _node;//定义父亲节点。Node* parent = cur->_parent;//如果当前节点不是父亲的右孩子，并且父亲是不存在，那么就是根节点或者是左孩子节点了//那就不进入循环。while (parent && cur == parent->_right){//如果是，那就往上找到下一个节点。cur = cur->_parent;parent = parent->_parent;}//更新节点_node = parent;}return *this;}bool operator!=(const Self& s){return _node != s._node;}
};
//跟节点的定义一样
//因为关联式容器中存储的是<key, value>的键值对，因此
// k为key的类型，
// ValueType: 如果是map，则为pair<K, V>; 如果是set，则为k。如下：
// map->RBTree<K,pair<const K,V>,MapKeyOfT> _t;
// set->RBTree<K,K,SetKeyOfT> _t
// 
// KeyOfValue: 通过value来获取key的一个仿函数类。其作用就是用于比较。
template<class K,class ValueType,class KeyOfValue>
class RBTree
{typedef RBTreeNode<ValueType> Node;
public:typedef __RBTreeIterator<ValueType> iterator;iterator begin(){Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);}iterator end(){return iterator(nullptr);}bool Insert(const ValueType& data){//先按二叉搜索树的规矩来创建一棵二叉搜索树if (_root == nullptr){_root = new Node(data);//因为红黑树的根节点是黑色的_root->_col = BLACK;return true;}KeyOfValue kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);cur->_col = RED;//多写一步，防止写错代码。if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//创建完二叉搜索树//开始创建红黑树，使用颜色来判断是否需要调整//循环往上走，循环条件：当走到的parent不为空，并且parent是红色的//即我们列举是三种情况，parent都是红的，就需要重新调整//如果parent是黑色的，那就不需要了。直接就是一棵红黑树,不进入循环while (parent && parent->_col == RED){//保存祖先节点，即g节点Node* grandfther = parent->_parent;//判断父节点是在祖先节点的哪边if (parent == grandfther->_left){//父节点在左边，那么叔叔节点就在右边Node* uncle = grandfther->_right;//情况一：uncle存在且为红。改变颜色即可if (uncle && uncle->_col == RED){//变色。parent->_col = uncle->_col = BLACK;grandfther->_col = RED;//往上走cur = grandfther;parent = cur->_parent;}else  //uncle不存在 或者 存在但是黑色{//情况二  p是g的左孩子，cur是p的左孩子，以g为轴右单旋if (cur == parent->_left){//右单旋RotateR(grandfther);//变色  右单旋后，parent为根节点，变黑色。cur和g节点为红色parent->_col = BLACK;grandfther->_col = RED;}else  //情况三  p是g的左孩子，cur是p的右孩子.{//先以p为轴左旋转RotateL(parent);//变成情况二，再以g为轴右单旋RotateR(grandfther);//变色  cur变成根节点，为黑色。p和g是红色cur->_col = BLACK;grandfther->_col = RED;}break;}}else  //parent是在grandfther的右边{//叔叔节点就在祖先节点的左边Node* uncle = grandfther->_left;//情况一：uncle存在且为红。改变颜色即可if (uncle && uncle->_col == RED){//变色。parent->_col = uncle->_col = BLACK;grandfther->_col = RED;//往上走cur = grandfther;parent = cur->_parent;}else  //uncle不存在 或者 存在但是黑色{//情况二  p是g的右孩子，cur是p的右孩子。if (cur == parent->_right){//左单旋RotateL(grandfther);//变色  右单旋后，parent为根节点，变黑色。cur和g节点为红色parent->_col = BLACK;grandfther->_col = RED;}else  //情况三  p是g的右孩子，cur是p的左孩子.{//先以p为轴右旋转RotateR(parent);//变成情况二，再以g为轴左单旋RotateL(grandfther);//变色  cur变成根节点，为黑色。p和g是红色cur->_col = BLACK;grandfther->_col = RED;}break;}}}//最后将根节点置为黑_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);std::cout << root->_kv.first << ": " << root->_kv.second << std::endl;_Inorder(root->_right);}bool Check(Node* root, int blackNum, const int ref){if (root == nullptr){//cout << blackNum << endl;if (blackNum != ref){cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则：出现连续红色节点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root, 0, ref);}
private:Node* _root = nullptr;
};