新乡网站开发的公司电话口碑营销策略有哪些

数据结构：二叉树

二叉树

1.一些特殊的二叉树

1.满二叉树

满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是
说，如果==一个二叉树的层数为K，且结点总数是2^k-1== ，则它就是满二叉树。

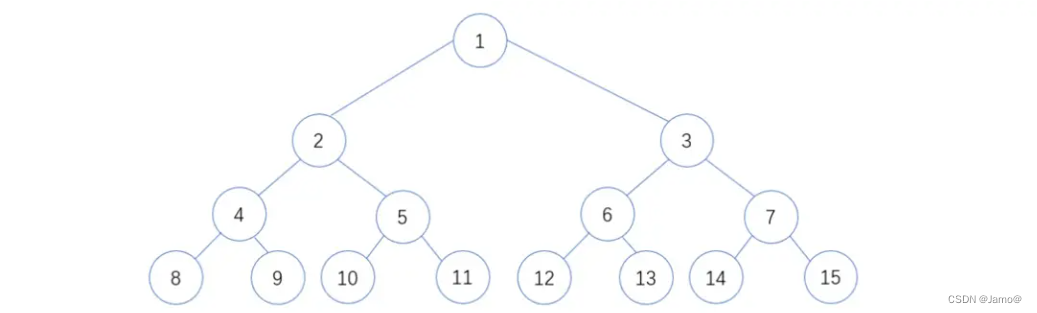
2.完全二叉树

完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K
的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一 一对
应时称之为完全二叉树。 **要注意的是满二叉树是一种特殊的完全二叉树**。

2.手动创建一颗二叉树

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>// 手动快速创建一棵简单的二叉树来测试三种深度优先遍历方式（前中后序遍历）（后续学习递归构建二叉树才是真正常用的方法）
typedef int BinaryTreeDataType;typedef struct BinaryTreeNode
{BinaryTreeDataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;BTNode* CreateBTNode(BinaryTreeDataType x)
{BTNode* NewBTNode = (BTNode*)malloc(sizeof(BTNode));if (NewBTNode == NULL){perror("malloc fail");exit(-1);}NewBTNode->val = x;NewBTNode->left = NULL;NewBTNode->right = NULL;return NewBTNode;
}
BTNode* CreatBinaryTree()
{BTNode* root = CreateBTNode(1);BTNode* node2 = CreateBTNode(2);BTNode* node3 = CreateBTNode(3);BTNode* node4 = CreateBTNode(4);BTNode* node5 = CreateBTNode(5);BTNode* node6 = CreateBTNode(6);root->left = node2;root->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return root;
}

3.二叉树深度优先遍历

前序、中序和后序遍历都属于「深度优先遍历 depth-first traversal, DFS」，它体现了一种“先走到尽头，再回溯继续”的遍历方式。

// 前序遍历
void Preorder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);Preorder(root->left);Preorder(root->right);
}// 中序遍历
void Inorder(BTNode* root)
{if (root == NULL){printf("N ");return;}Inorder(root->left);printf("%d ", root->val);Inorder(root->right);
}
// 后序遍历
void Postorder(BTNode* root)
{if (root == NULL){printf("N ");return;}Postorder(root->left);Postorder(root->right);printf("%d ", root->val);
}

4.二叉树层序遍历

层序遍历本质上属于「广度优先遍历 breadth-first traversal, BFS」，它体现了一种“一圈一圈向外扩展”的逐层遍历方式。

利用队列先进先出的性质：父亲先进队列，父亲出来时再带孩子进队列

void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列   实现二叉树的层序遍历   (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);while (!Empty(queuehead)){// 遍历二叉树入队列并挨个打印值BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}// 销毁队列Destroy(&queuehead);
}

5.二叉树基础操作

1.创建二叉树

typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
// 通过 前序遍历 的数组"ABD##E#H##CF##G##"构建二叉树BTNode* BinaryTreeCreate(BTDataType* parray, int* pi)
{// 前序遍历创建二叉树if (parray[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = parray[(*pi)++];root->left = BinaryTreeCreate(parray, pi);root->right = BinaryTreeCreate(parray, pi);return root;
}

2.二叉树节点个数

/*
写法一：遍历计数
*/
int BinaryTreeSize(BTNode* root)
{// 遍历二叉树计算节点个数static int size = 0;// 函数中使用静态不能完全解决问题，无法处理多次计算的情况if (root == NULL){return 0;}size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}/*
写法二：递归分治子问题
*/
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//节点个数 = 左子树节点个数 + 右子树节点个数 + 1
}

3.二叉树叶子节点个数

int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}// 叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数return root->left == NULL && root->right == NULL ? 1 : BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

4.二叉树的高度

/*
写法1：
*/
int BinaryTreeHight(BTNode* root)
{if (root == NULL){return 0;}// 此处递归分治多次重复导致效率过低(原因是此逻辑中比较时候进行了递归分治，计算的时候又重复进行了计算)return BinaryTreeHight(root->left) > BinaryTreeHight(root->right)|| BinaryTreeHight(root->left) == BinaryTreeHight(root->right)? BinaryTreeHight(root->left) + 1: BinaryTreeHight(root->right) + 1;// 二叉树的高度 = 左子树与右子树相比，高度更高的那棵树的高度 + 1
}/*
写法2：
*/
int BinaryTreeHight(BTNode* root)
{if (root == NULL){return 0;}//提前记录高度int lefthight = BinaryTreeHight(root->left);int righthight = BinaryTreeHight(root->right);// 二叉树的高度 = 左子树与右子树相比，高度更高的那棵树的高度 + 1return lefthight > righthight|| lefthight == righthight? lefthight + 1: righthight + 1;}

5.二叉树第k层节点个数

int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (root != NULL && k == 1){return 1;}// 问题拆分：第k层节点个数 = 左子树第k-1层节点数 + 右子树第k-层节点数return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);}

6.二叉树查找值为x的节点

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}// 前序遍历二叉树寻找该节点if (root->data == x){return root;}else{BTNode* leftnode = BinaryTreeFind(root->left, x);if (leftnode){return leftnode;}BTNode* rightnode = BinaryTreeFind(root->right, x);if (rightnode){return rightnode;}//如果左右节点都不是我们要找的该节点则返回空if (leftnode == NULL && rightnode == NULL){return NULL;}}
}

7.层序遍历

void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列   实现二叉树的层序遍历   (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);while (!Empty(queuehead)){// 遍历二叉树入队列并挨个打印值BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}// 销毁队列Destroy(&queuehead);
}

变形：如何控制一层一层打印并换行？

// 层序遍历变形换行打印
void BinaryTreeLevelOrder(BTNode* root)
{// 利用队列   实现二叉树的层序遍历   (队列先进先出性质)Queue* queuehead = Init();Push(&queuehead, root);// 根据每一层的数据的个数得出打印多少次后进行一次换行int levelsize = 1;while (!Empty(queuehead)){// 一层一层出while (levelsize--){// 遍历二叉树入队列BTNode* front = Peek(&queuehead);printf("%c ", front->data);Pop(&queuehead);if (front->left != NULL){Push(&queuehead, front->left);}if (front->right != NULL){Push(&queuehead, front->right);}}printf("\n");levelsize = Size(queuehead);}// 销毁队列Destroy(&queuehead);
}

8.二叉树销毁

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{// 走后序遍历更方便销毁if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}

9.判断二叉树是否是完全二叉树

思路：完全二叉树只有最后一层会出现 NULL 值，而且出现了 NULL 值，则后面不会再出现非空的值。我们可以通过层序遍历的思想，一层一层遍历，如果遇到空结点，记录一下，然后继续遍历，若是后面出现了非空值，则说明该二叉树不是完全二叉树。

// 判断二叉树是否是完全二叉树
// 参数：root，一个指向二叉树根节点的指针
bool BinaryTreeComplete(BTNode* root)
{Queue* queuehead = Init();// 将二叉树的根节点入队列Push(&queuehead, root);while (!Empty(queuehead)){BTNode* front = Peek(&queuehead);if (front == NULL){break;}Pop(&queuehead);Push(&queuehead, front->left);Push(&queuehead, front->right);}// 当第一次遍历的时候出道空代表应当结束了，第二次继续往后遍历如果队列中还有非空代表不是完全二叉树while (!Empty(queuehead)){BTNode* front = Peek(&queuehead);Pop(&queuehead);if (front != NULL){return false;}}return true;
}