当前位置： 首页 > news >正文

网站开发学习网信阳网站推广公司

news 2025/7/17 21:06:17
网站开发学习网,信阳网站推广公司,温州网站建设有限公司,软件开发包括哪些数值运算相关 一、概述二、常用数学函数1. 基础运算1. 浮点值的绝对值（ |x| ）2. 浮点除法运算的余数3. 除法运算的有符号余数4. 除法运算的有符号余数和最后三个二进制位5. 混合的乘加运算6. 两个浮点值的较大者7. 两个浮点值的较小者8. 两个浮点值的正数…

数值运算相关

  • 一、概述
  • 二、常用数学函数
    • 1. 基础运算
      • 1. 浮点值的绝对值（ |x| ）
      • 2. 浮点除法运算的余数
      • 3. 除法运算的有符号余数
      • 4. 除法运算的有符号余数和最后三个二进制位
      • 5. 混合的乘加运算
      • 6. 两个浮点值的较大者
      • 7. 两个浮点值的较小者
      • 8. 两个浮点值的正数差（ max(0, x-y) ）
    • 2. 指数函数
      • 1. 返回 e 的给定次幂（ e^x^ ）
      • 2. 返回 2 的给定次幂（ 2^x^ ）
      • 3. 返回 e 的给定次幂减一（ e^x^-1 ）
      • 4. 自然（以 e 为底）对数（ ln(x) ）
      • 5. 常用（以 10 为底）对数（ log~10~(x) ）
      • 6. 给定数值的以 2 为底的对数（ log~2~(x) ）
      • 7. 加上给定数值的自然（以 e 为底）对数（ ln(1+x) ）
    • 3. 幂函数
      • 1. 求某数的给定次幂（ x^y^ ）
      • 2. 计算平方根（ √x ）
      • 3. 计算立方根（ 3√x ）
      • 4. 计算两个给定数的平方和的平方根（ √x^2^+y^2^ ）
    • 4. 三角函数
      • 1. 计算正弦（ sin(x) ）
      • 2. 计算余弦（ cos(x) ）
      • 3. 计算正切（ tan(x) ）
      • 4. 计算反正弦（ arcsin(x) ）
      • 5. 计算反余弦（ arccos(x) ）
      • 6. 计算反正切（ arctan(x) ）
      • 7. 反正切，用符号确定象限
    • 5. 双曲函数
      • 1. 计算双曲正弦（ sinh(x) ）
      • 2. 计算双曲余弦（ cosh(x) ）
      • 3. 计算双曲正切（ tanh(x) ）
      • 4. 计算反双曲正弦（ arsinh(x) ）
      • 5. 计算反双曲余弦（ arcosh(x) ）
      • 6. 计算反双曲正切（ artanh(x) ）
    • 6. 误差与伽马函数
      • 1. 误差函数
      • 2. 补误差函数
      • 3. gamma 函数
      • 4. gamma 函数的自然对数
    • 7. 最接近整数的浮点运算
      • 1. 不小于给定值的最接近整数值
      • 2. 不大于给定值的最接近整数
      • 3. 绝对值不大于给定值的最接近整数
      • 4. 最接近整数，中间情况下向远离零舍入
      • 5. 使用当前舍入模式的最接近整数
      • 6. 使用当前舍入模式的最接近整数
    • 8. 浮点操作函数
    • 9. 分类与比较
  • 三、宏常量
  • 四、错误处理

一、概述

C++为我们提供了很多已经定义好的一些数学函数，这些函数的使用一定要注意函数的定义域，因为计算机表示的数据有限，有些非法的运算的结果也是在数值运算库中定义好了的。

二、常用数学函数

在标准库中基本上提供了对于 float、double、long double 类型参数的输入、也有对应的参数 float、double、long double 的输出。就像下面的可以看得出来 不带 任何的后缀是有3个类型的重载、带 ‘f’ 的指定了强制 float 类型、带 ‘l’ 的强制指定了 long double 类型。基本上下面提到的函数都会有这些后缀以满足不同精度的需求。

float       	fmod ( float x, float y );
double      	fmod ( double x, double y );
long double 	fmod ( long double x, long double y );  float       	fmodf( float x, float y );
long double 	fmodl( long double x, long double y );

1. 基础运算

1. 浮点值的绝对值（ |x| ）

基础定义： 就是求一个数值的绝对值

double  abs( double arg );

abs(float x)
fabs
fabsf
fabsl

此函数不受制于任何指定于 math_errhandling 的错误条件。

若实现支持 IEEE 浮点算术（ IEC 60559 ），则

  • 若输入参数为 ±0 ，则返回 +0
  • 若输入参数为 ±∞ ，则返回 +∞
  • 若输入参数为 NaN ，则返回 NaN

示例：

#include <iostream>
#include <cmath>int main()
{std::cout << "abs(+3.0) = " << std::abs(+3.0) << '\n'<< "abs(-3.0) = " << std::abs(-3.0) << '\n';// 特殊值std::cout << "abs(-0.0) = " << std::abs(-0.0) << '\n'<< "abs(-Inf) = " << std::abs(-INFINITY) << '\n'<< "abs(-NaN) = " << std::abs(-NAN) << '\n';
}
//输出
abs(+3.0) = 3
abs(-3.0) = 3
abs(-0.0) = 0
abs(-Inf) = inf
abs(-NaN) = nan

2. 浮点除法运算的余数

基础定义：计算除法运算 x/y 的浮点余数。有点像整数的余数运算符 %

double fmod ( double x, double y );

fmod
fmodf
fmodl

#include <iostream>
#include <cmath>
#include <cfenv>#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "fmod(+5.1, +3.0) = " << std::fmod(5.1,3) << '\n'<< "fmod(-5.1, +3.0) = " << std::fmod(-5.1,3) << '\n'<< "fmod(+5.1, -3.0) = " << std::fmod(5.1,-3) << '\n'<< "fmod(-5.1, -3.0) = " << std::fmod(-5.1,-3) << '\n';// 特殊值std::cout << "fmod(+0.0, 1.0) = " << std::fmod(0, 1) << '\n'<< "fmod(-0.0, 1.0) = " << std::fmod(-0.0, 1) << '\n'<< "fmod(5.1, Inf) = " << std::fmod(5.1, INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fmod(+5.1, 0) = " << std::fmod(5.1, 0) << '\n';if(std::fetestexcept(FE_INVALID))std::cout << "    FE_INVALID raised\n";
}
// 输出
fmod(+5.1, +3.0) = 2.1
fmod(-5.1, +3.0) = -2.1
fmod(+5.1, -3.0) = 2.1
fmod(-5.1, -3.0) = -2.1
fmod(+0.0, 1.0) = 0
fmod(-0.0, 1.0) = -0
fmod(5.1, Inf) = 5.1
fmod(+5.1, 0) = -nanFE_INVALID raised

3. 除法运算的有符号余数

基础定义：此函数所计算的除法运算 x/y 的 IEEE 浮点余数，准确地为值 x - n*y ，其中值 n 是最接近 x/y 准确值的整数值。 |n-x/y| = ½ 时，选择作为偶数的 n 。与 std::fmod() 相反，不保证返回值拥有与 x 相同的符号。若返回值是 0 ，则它拥有与 x 相同的符号。

double      remainder ( double x, double y );

remainder
remainderf
remainderl

#include <iostream>
#include <cmath>
#include <cfenv>#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "remainder(+5.1, +3.0) = " << std::remainder(5.1,3) << '\n'<< "remainder(-5.1, +3.0) = " << std::remainder(-5.1,3) << '\n'<< "remainder(+5.1, -3.0) = " << std::remainder(5.1,-3) << '\n'<< "remainder(-5.1, -3.0) = " << std::remainder(-5.1,-3) << '\n';// 特殊值std::cout << "remainder(-0.0, 1.0) = " << std::remainder(-0.0, 1) << '\n'<< "remainder(5.1, Inf) = " << std::remainder(5.1, INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "remainder(+5.1, 0) = " << std::remainder(5.1, 0) << '\n';if(fetestexcept(FE_INVALID))std::cout << "    FE_INVALID raised\n";
}
//输出
remainder(+5.1, +3.0) = -0.9
remainder(-5.1, +3.0) = 0.9
remainder(+5.1, -3.0) = -0.9
remainder(-5.1, -3.0) = 0.9
remainder(-0.0, 1.0) = -0
remainder(5.1, Inf) = 5.1
remainder(+5.1, 0) = -nanFE_INVALID raised

4. 除法运算的有符号余数和最后三个二进制位

基础定义：
remquo
remquof
remquol

5. 混合的乘加运算

基础定义：计算 (x*y) + z ，如同用无限精度，而仅舍入一次到结果类型。

double      fma ( double x, double y, double z );

fma
fmaf
fmal

#include <iostream>
#include <iomanip>
#include <cmath>
#include <cfenv>
#pragma STDC FENV_ACCESS ON
int main()
{// 演示 fma 与内建运算符间的差别double in = 0.1;std::cout << "0.1 double is " << std::setprecision(23) << in<< " (" << std::hexfloat << in << std::defaultfloat << ")\n"<< "0.1*10 is 1.0000000000000000555112 (0x8.0000000000002p-3), "<< "or 1.0 if rounded to double\n";double expr_result = 0.1 * 10 - 1;double fma_result = fma(0.1, 10, -1);std::cout << "0.1 * 10 - 1 = " << expr_result<< " : 1 subtracted after intermediate rounding\n"<< "fma(0.1, 10, -1) = " << std::setprecision(6) << fma_result << " ("<< std::hexfloat << fma_result << std::defaultfloat << ")\n\n";// fma 用于 double-double 算术double high = 0.1 * 10;double low = fma(0.1, 10, -high);std::cout << "in double-double arithmetic, 0.1 * 10 is representable as "<< high << " + " << low << "\n\n";// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fma(+Inf, 10, -Inf) = " << std::fma(INFINITY, 10, -INFINITY) << '\n';if(std::fetestexcept(FE_INVALID))std::cout << "    FE_INVALID raised\n";
}
//输出
0.1 double is 0.10000000000000000555112 (0x1.999999999999ap-4)
0.1*10 is 1.0000000000000000555112 (0x8.0000000000002p-3), or 1.0 if rounded to double
0.1 * 10 - 1 = 0 : 1 subtracted after intermediate rounding
fma(0.1, 10, -1) = 5.55112e-17 (0x1p-54)in double-double arithmetic, 0.1 * 10 is representable as 1 + 5.55112e-17fma(+Inf, 10, -Inf) = -nanFE_INVALID raised

6. 两个浮点值的较大者

基础定义：返回二个浮点数的较大者

double      fmax ( double x, double y );

fmax
fmaxf
fmaxl


#include <iostream>
#include <cmath>int main()
{std::cout << "fmax(2,1)    = " << std::fmax(2,1) << '\n'<< "fmax(-Inf,0) = " << std::fmax(-INFINITY,0) << '\n'<< "fmax(NaN,-1) = " << std::fmax(NAN,-1) << '\n';
}
//输出：
fmax(2,1)    = 2
fmax(-Inf,0) = 0
fmax(NaN,-1) = -1

7. 两个浮点值的较小者

基础定义：返回二个浮点数的较小者

double      fmin ( double x, double y );

fmin
fminf
fminl

#include <iostream>
#include <cmath>int main()
{std::cout << "fmin(2,1)    = " << std::fmin(2,1) << '\n'<< "fmin(-Inf,0) = " << std::fmin(-INFINITY,0) << '\n'<< "fmin(NaN,-1) = " << std::fmin(NAN,-1) << '\n';
}
//输出
fmin(2,1)    = 1
fmin(-Inf,0) = -inf
fmin(NaN,-1) = -1

8. 两个浮点值的正数差（ max(0, x-y) ）

基础定义：返回 x 与 y 间的正差，即若 x>y 则返回 x-y ，否则（若 x≤y ）返回 +0 。

double      fdim ( double x, double y );

fdim
fdimf
fdiml

#include <iostream>
#include <cmath>
#include <cerrno>
#include <cstring>
#include <cfenv>
#pragma STDC FENV_ACCESS ON
int main()
{std::cout << "fdim(4, 1) = " << std::fdim(4, 1)<< " fdim(1, 4) = " << std::fdim(1, 4) << '\n'<< "fdim(4,-1) = " << std::fdim(4, -1)<< " fdim(1,-4) = " << std::fdim(1, -4) << '\n';// 错误处理errno = 0;std::feclearexcept(FE_ALL_EXCEPT);std::cout << "fdim(1e308, -1e308) = " << std::fdim(1e308, -1e308) << '\n';if (errno == ERANGE)std::cout << "    errno == ERANGE: " << std::strerror(errno) << '\n';if (std::fetestexcept(FE_OVERFLOW))std::cout << "    FE_OVERFLOW raised\n";
}
//输出
fdim(4, 1) = 3 fdim(1, 4) = 0
fdim(4,-1) = 5 fdim(1,-4) = 5
fdim(1e308, -1e308) = inferrno == ERANGE: Numerical result out of rangeFE_OVERFLOW raised

2. 指数函数

1. 返回 e 的给定次幂（ ex ）

基础定义

double      exp ( double arg );

exp
expf
expl

图像
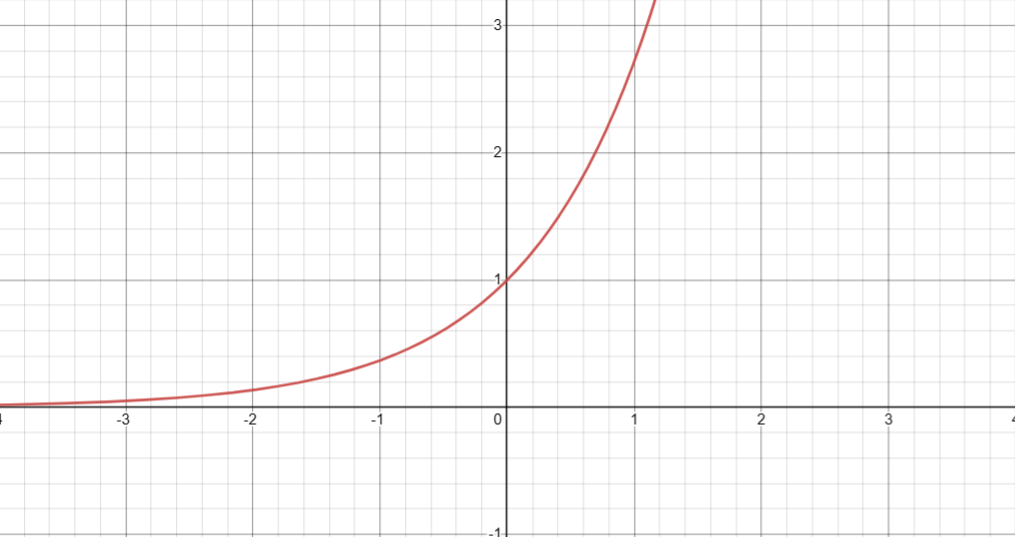
在这里插入图片描述

2. 返回 2 的给定次幂（ 2x ）

基础定义

double      exp2 ( double n );

exp2
exp2f
exp2l

图像

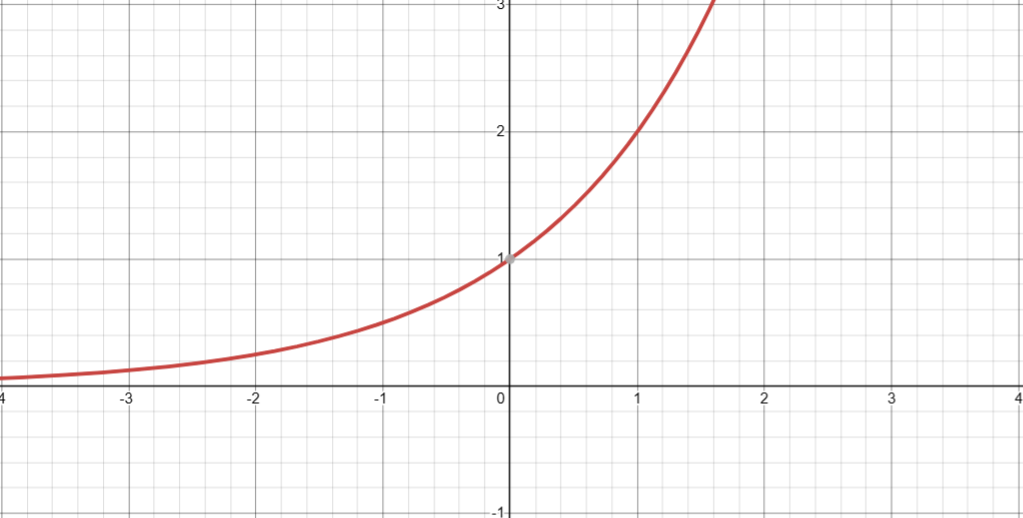
在这里插入图片描述

3. 返回 e 的给定次幂减一（ ex-1 ）

基础定义：

double      expm1 ( double arg );`在这里插入代码片`

expm1
expm1f
expm1l

图像
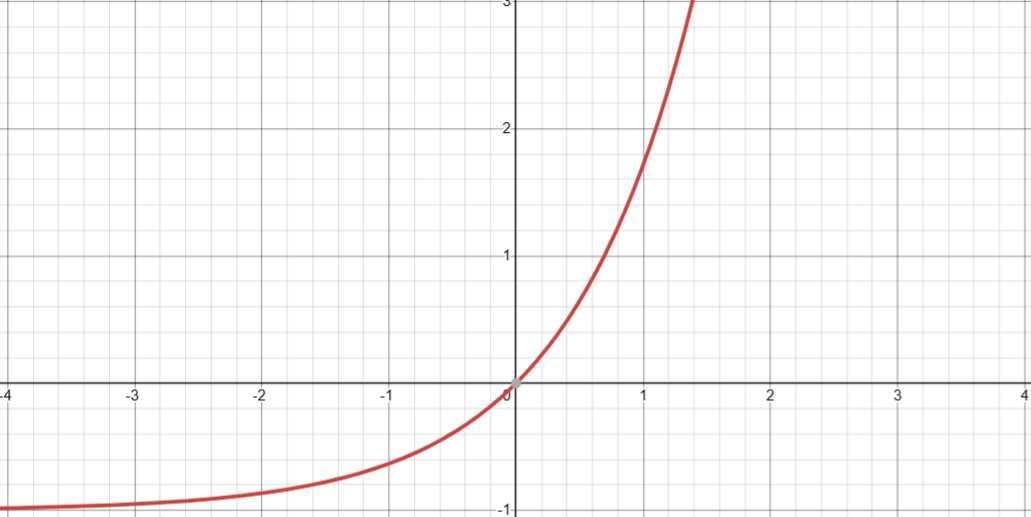
在这里插入图片描述

4. 自然（以 e 为底）对数（ ln(x) ）

基础定义

double      log ( double arg );

log
logf
logl

图像
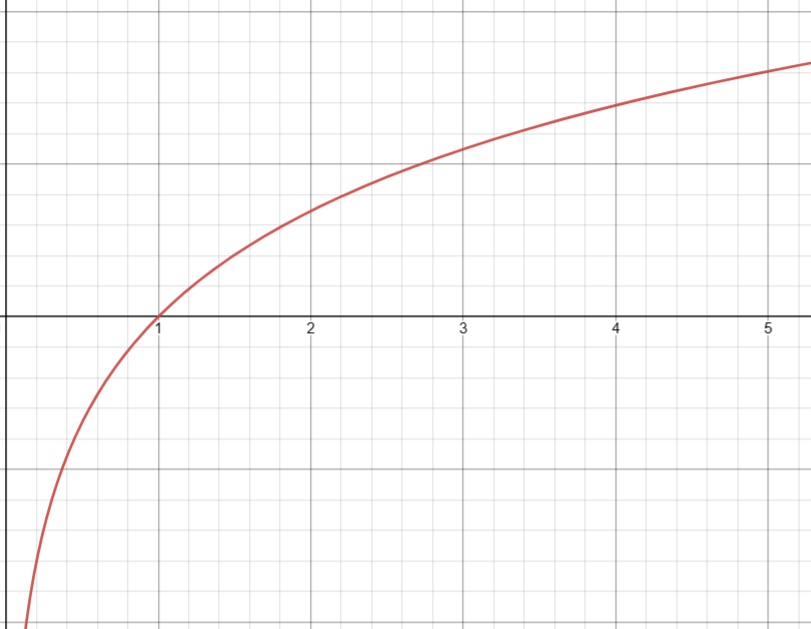
在这里插入图片描述

5. 常用（以 10 为底）对数（ log10(x) ）

基础定义

double      log10 ( double arg );

log10
log10f
log10l

图像
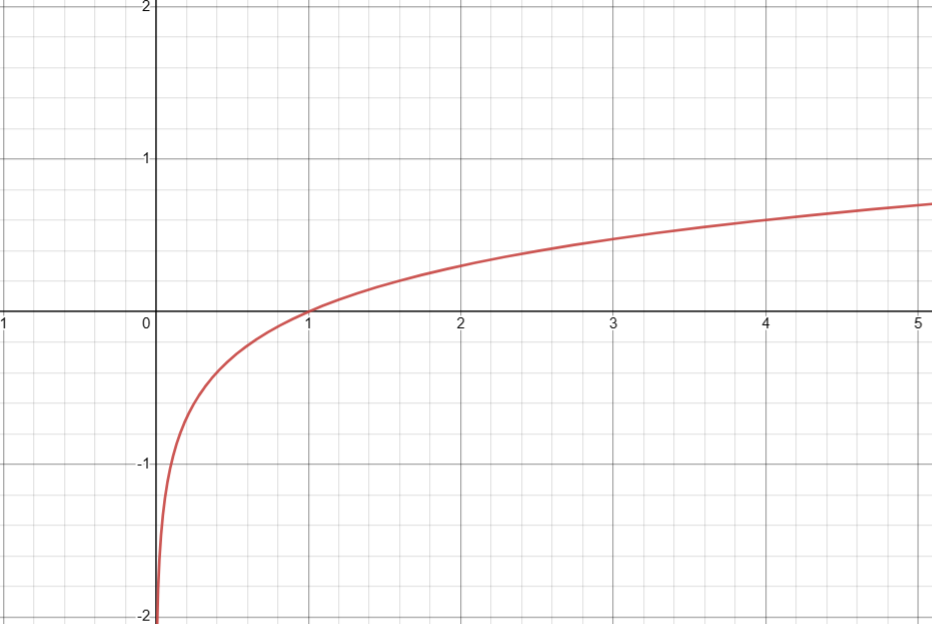
在这里插入图片描述

6. 给定数值的以 2 为底的对数（ log2(x) ）

基础定义

double      log2 ( double arg );

log2
log2f
log2l

图像
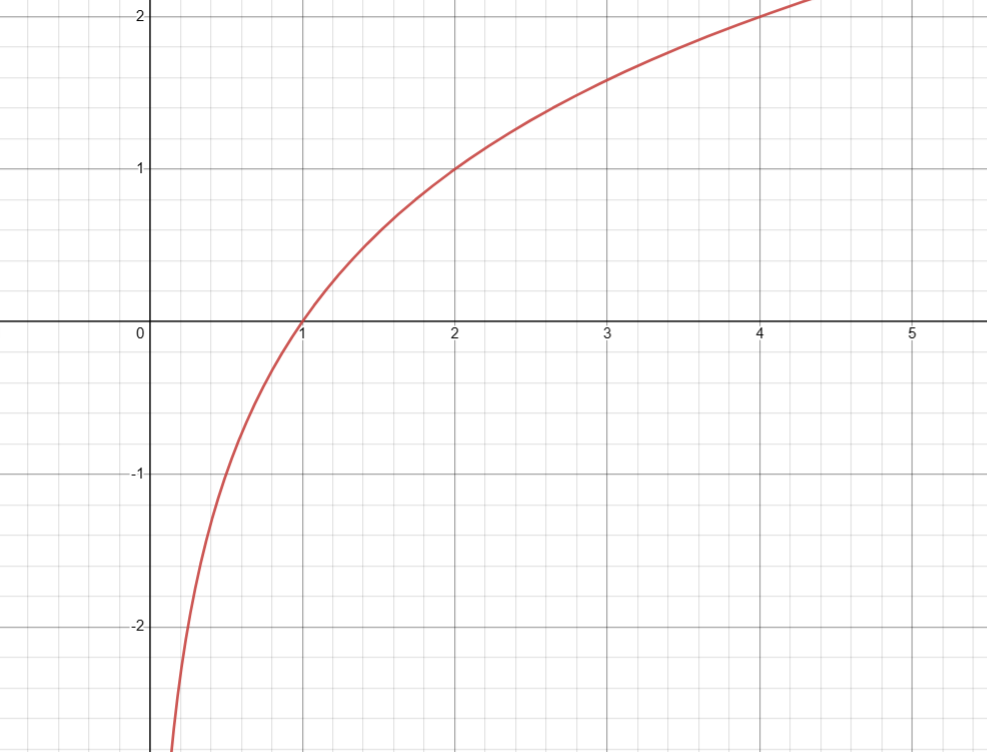
在这里插入图片描述

7. 加上给定数值的自然（以 e 为底）对数（ ln(1+x) ）

基础定义

double      log1p ( double arg );

log1p
log1pf
log1pl

图像
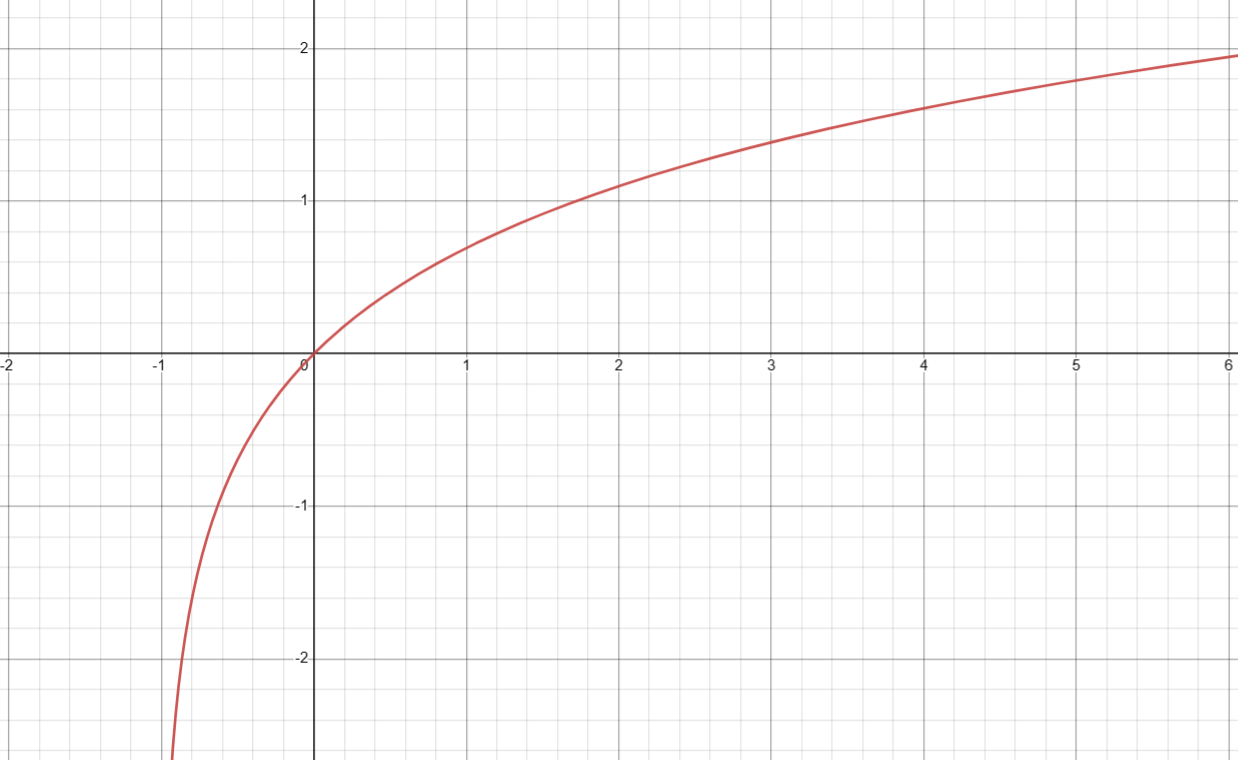
在这里插入图片描述

3. 幂函数

1. 求某数的给定次幂（ xy ）

基础定义

double      pow ( double base, double exp );

pow
powf
powl

2. 计算平方根（ √x ）

基础定义

double      sqrt ( double arg );

sqrt
sqrtf
sqrtl

3. 计算立方根（ 3√x ）

基础定义

double      cbrt ( double arg );

cbrt
cbrtf
cbrtl

4. 计算两个给定数的平方和的平方根（ √x2+y2 ）

基础定义

double      hypot ( double x, double y );

hypot
hypotf
hypotl

4. 三角函数

1. 计算正弦（ sin(x) ）

基础定义

double      sin ( double arg );

sin
sinf
sinl

图像
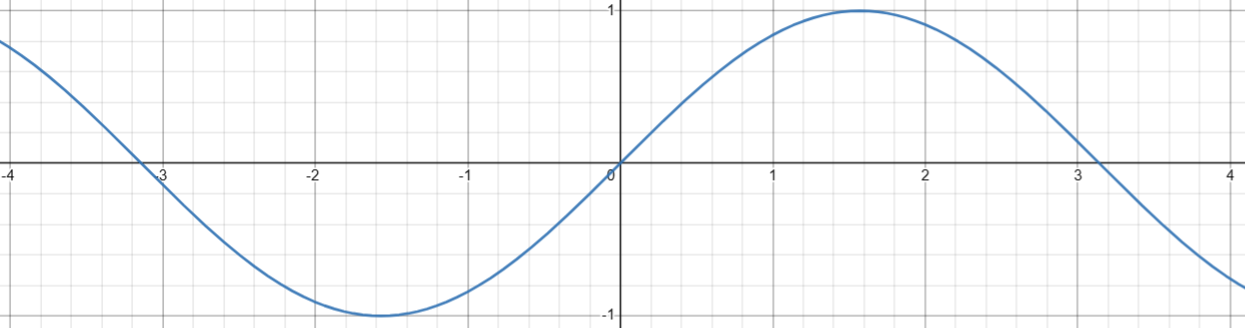
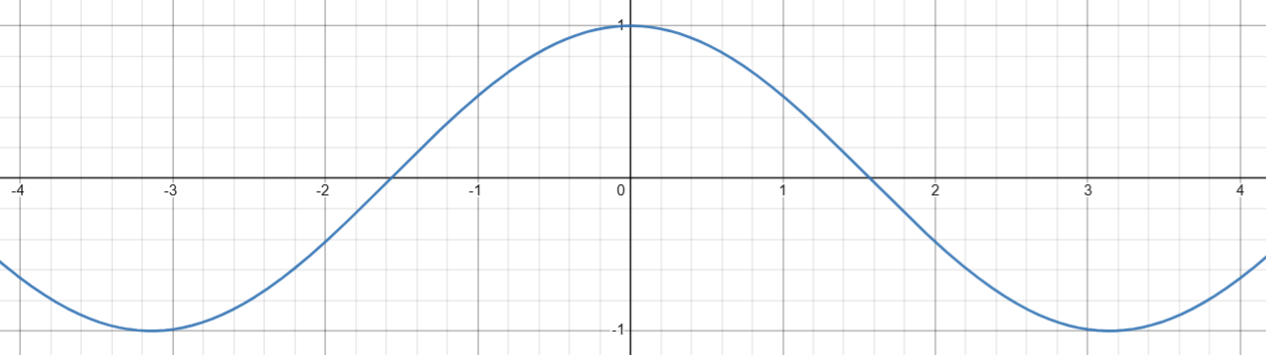
在这里插入图片描述

2. 计算余弦（ cos(x) ）

基础定义

double      cos ( double arg );

cos
cosf
cosl

图像
在这里插入图片描述

3. 计算正切（ tan(x) ）

基础定义

double      tan ( double arg );

tan
tanf
tanl

图像
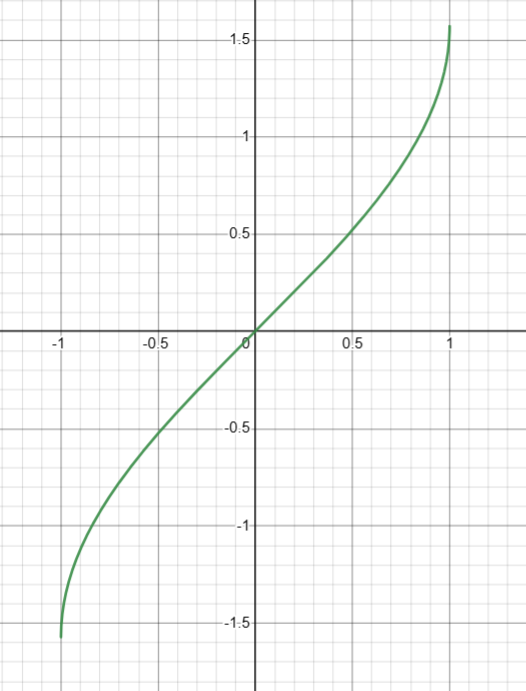
在这里插入图片描述

4. 计算反正弦（ arcsin(x) ）

基础定义

double      asin ( double arg );

asin
asinf
asinl

图像
在这里插入图片描述

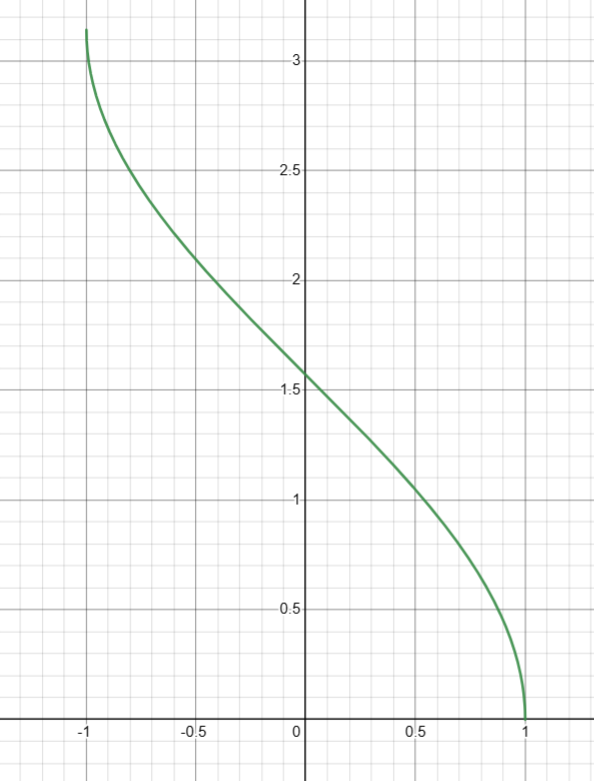
5. 计算反余弦（ arccos(x) ）

基础定义

double      acos ( double arg );

acos
acosf
acosl

图像
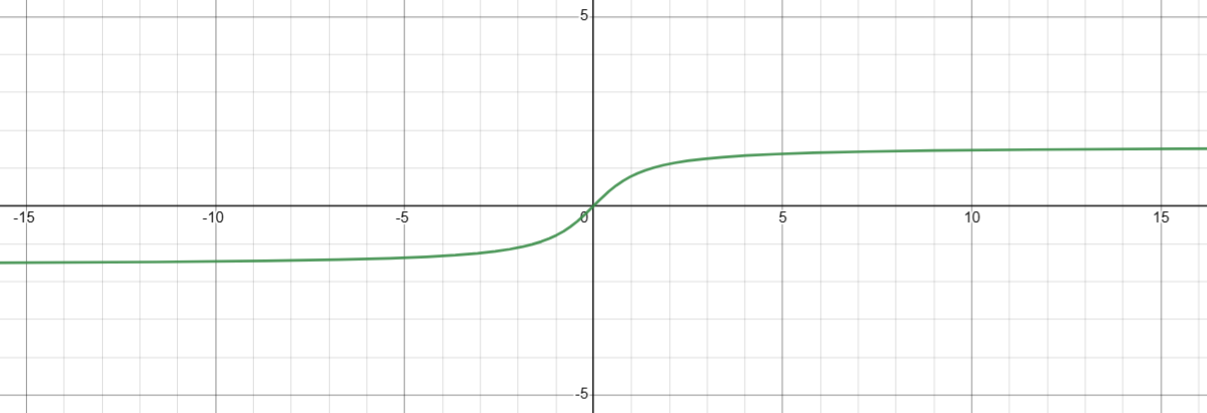
在这里在这里插入图片描述 插入图片描述

6. 计算反正切（ arctan(x) ）

基础定义

double      atan ( double arg );

atan
atanf
atanl

图像
在这里插入图片描述

7. 反正切，用符号确定象限

基础定义

double      atan2 ( double y, double x );

atan2
atan2f
atan2l

5. 双曲函数

1. 计算双曲正弦（ sinh(x) ）

基础定义

double      sinh ( double arg );

sinh
sinhf
sinhl

图像
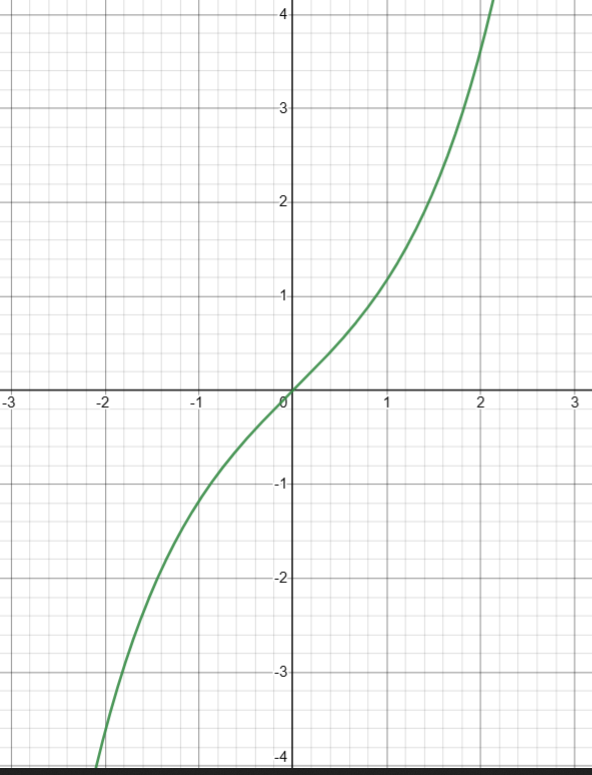
在这里插入图片描述

2. 计算双曲余弦（ cosh(x) ）

基础定义

double      cosh ( double arg );

cosh
coshf
coshl

图像
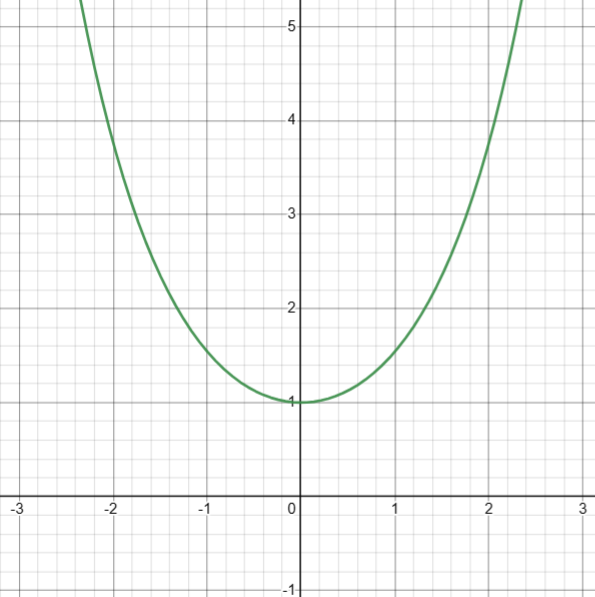
在这里插入图片描述

3. 计算双曲正切（ tanh(x) ）

基础定义

double      tanh ( double arg );

tanh
tanhf
tanhl

图像
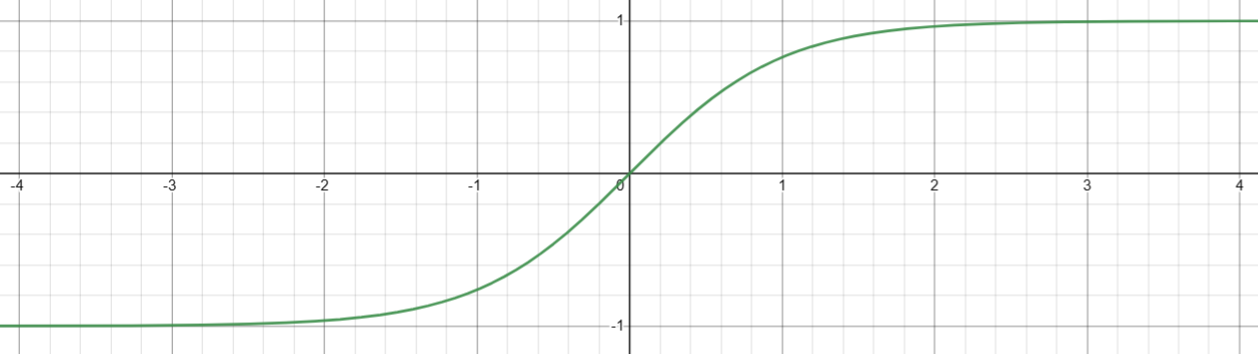
在这里插入图片描述

4. 计算反双曲正弦（ arsinh(x) ）

基础定义

double      asinh ( double arg );

asinh
asinhf
asinhl

图像
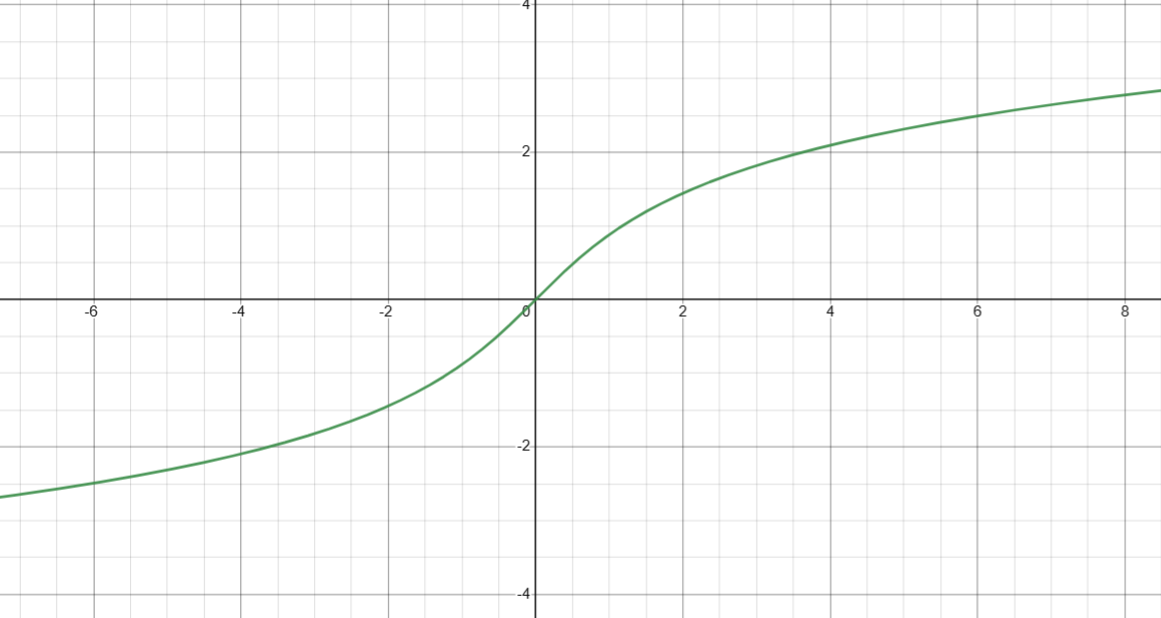
在这里插入图片描述

5. 计算反双曲余弦（ arcosh(x) ）

基础定义

double      acosh ( double arg );

acosh
acoshf
acoshl

图像
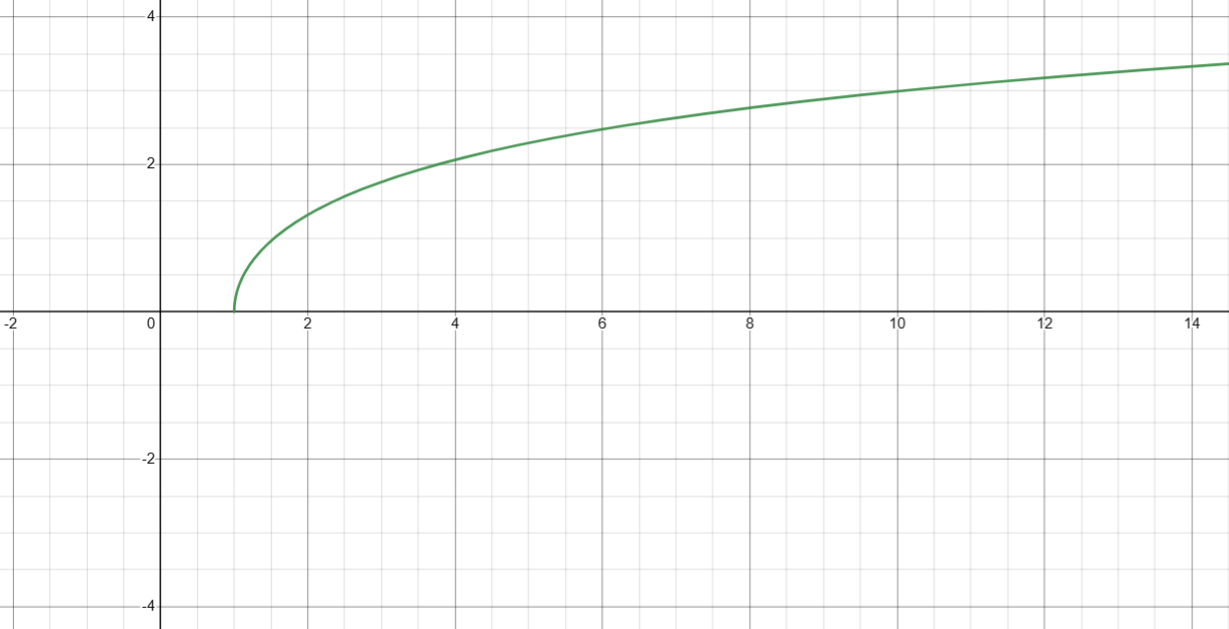
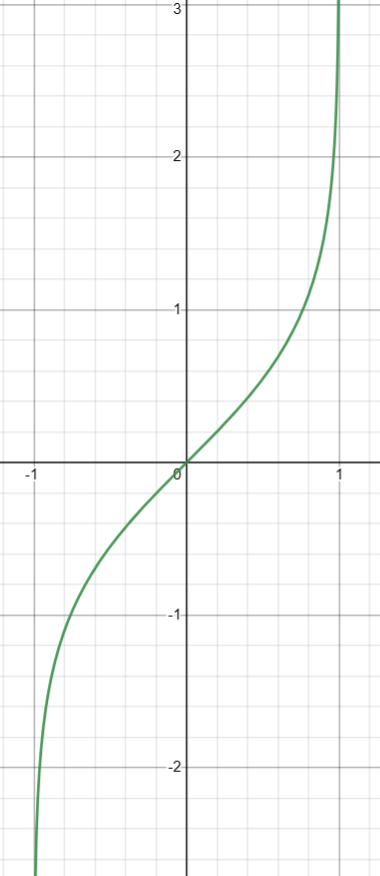
在这里插入图片描述

6. 计算反双曲正切（ artanh(x) ）

基础定义

double      atanh ( double arg );

atanh
atanhf
atanhl

图像
在这里插入图片描述

6. 误差与伽马函数

1. 误差函数

erf
erff
erfl

2. 补误差函数

erfc
erfcf
erfcl

3. gamma 函数

tgamma
tgammaf
tgammal

4. gamma 函数的自然对数

lgamma
lgammaf
lgammal

7. 最接近整数的浮点运算

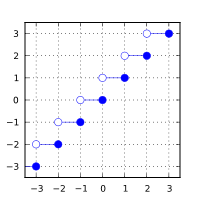
1. 不小于给定值的最接近整数值

基础定义：计算不小于 arg 的最小整数值。

double      ceil ( double arg );

ceil
ceilf
ceill
在这里插入图片描述

#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "floor(+2.7) = " << std::floor(+2.7) << '\n'<< "floor(-2.7) = " << std::floor(-2.7) << '\n'<< "floor(-0.0) = " << std::floor(-0.0) << '\n'<< "floor(-Inf) = " << std::floor(-INFINITY) << '\n';
}//输出：
floor(+2.7) = 2.000000
floor(-2.7) = -3.000000
floor(-0.0) = -0.000000
floor(-Inf) = -inf

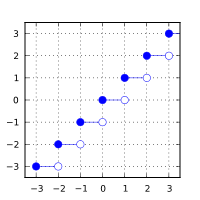
2. 不大于给定值的最接近整数

基础定义：计算不大于 arg 的最大整数值。
在这里插入图片描述

#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "floor(+2.7) = " << std::floor(+2.7) << '\n'<< "floor(-2.7) = " << std::floor(-2.7) << '\n'<< "floor(-0.0) = " << std::floor(-0.0) << '\n'<< "floor(-Inf) = " << std::floor(-INFINITY) << '\n';
}//输出：
floor(+2.7) = 2.000000
floor(-2.7) = -3.000000
floor(-0.0) = -0.000000
floor(-Inf) = -inf

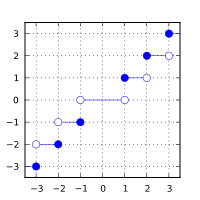
3. 绝对值不大于给定值的最接近整数

基础定义：计算绝对值不大于 arg 的最接近整数。
在这里插入图片描述

#include <cmath>
#include <iostream>
int main()
{std::cout << std::fixed<< "trunc(+2.7) = " << std::trunc(+2.7) << '\n'<< "trunc(-2.9) = " << std::trunc(-2.9) << '\n'<< "trunc(-0.0) = " << std::trunc(-0.0) << '\n'<< "trunc(-Inf) = " << std::trunc(-INFINITY) << '\n';
}// 可能的输出：
trunc(+2.7) = 2.000000
trunc(-2.9) = -2.000000
trunc(-0.0) = -0.000000
trunc(-Inf) = -inf

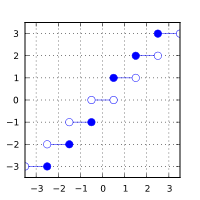
4. 最接近整数，中间情况下向远离零舍入

基础定义：计算 arg 的最接近整数值（以浮点格式），中点情况舍入为远离零，无关乎当前舍入模式。 计算 arg 的最接近整数值（以整数格式），中点情况舍入为远离零，无关乎当前舍入模式。
在这里插入图片描述

#include <iostream>
#include <cmath>
#include <cfenv>
#include <climits>#pragma STDC FENV_ACCESS ONint main()
{// roundstd::cout << "round(+2.3) = " << std::round(2.3)<< "  round(+2.5) = " << std::round(2.5)<< "  round(+2.7) = " << std::round(2.7) << '\n'<< "round(-2.3) = " << std::round(-2.3)<< "  round(-2.5) = " << std::round(-2.5)<< "  round(-2.7) = " << std::round(-2.7) << '\n';std::cout << "round(-0.0) = " << std::round(-0.0)  << '\n'<< "round(-Inf) = " << std::round(-INFINITY) << '\n';// lroundstd::cout << "lround(+2.3) = " << std::lround(2.3)<< "  lround(+2.5) = " << std::lround(2.5)<< "  lround(+2.7) = " << std::lround(2.7) << '\n'<< "lround(-2.3) = " << std::lround(-2.3)<< "  lround(-2.5) = " << std::lround(-2.5)<< "  lround(-2.7) = " << std::lround(-2.7) << '\n';std::cout << "lround(-0.0) = " << std::lround(-0.0)  << '\n'<< "lround(-Inf) = " << std::lround(-INFINITY) << '\n';// 错误处理std::feclearexcept(FE_ALL_EXCEPT);std::cout << "std::lround(LONG_MAX+1.5) = "<< std::lround(LONG_MAX+1.5) << '\n';if (std::fetestexcept(FE_INVALID))std::cout << "    FE_INVALID was raised\n";
}//可能的输出：
round(+2.3) = 2  round(+2.5) = 3  round(+2.7) = 3
round(-2.3) = -2  round(-2.5) = -3  round(-2.7) = -3
round(-0.0) = -0
round(-Inf) = -inf
lround(+2.3) = 2  lround(+2.5) = 3  lround(+2.7) = 3
lround(-2.3) = -2  lround(-2.5) = -3  lround(-2.7) = -3
lround(-0.0) = 0
lround(-Inf) = -9223372036854775808
std::lround(LONG_MAX+1.5) = -9223372036854775808FE_INVALID was raised

5. 使用当前舍入模式的最接近整数

6. 使用当前舍入模式的最接近整数

若结果有别则有异常

8. 浮点操作函数

9. 分类与比较

三、宏常量

四、错误处理

http://www.hrbkazy.com/news/40665.html

相关文章：

  • 个人站长怎么做企业网站百度推广登录首页网址
  • 织梦网站如何做地区分站百度注册网站
  • 安徽设计网站建设佳木斯seo
  • 做社交网站 投入网站seo外包公司
  • 雨岑信息科技有限公司做企业型网站做的怎么样_公司规模如何百度地图导航网页版
  • 无锡网站建设无锡速联科技世界杯竞猜
  • 建一个鲜花买卖网站多少钱网络seo培训
  • 网站设计网站播放视频速度优化
  • 公司使用威联通nas做网站存储软件商店安装
  • 扬州网站建设5118网站如何使用免费版
  • wordpress 腾讯qq登陆seo交流群
  • 公司logo设计注意事项seo入门教程
  • 搞钱的路子网站百度ai助手入口
  • 被墙的网站有哪些建网站需要什么条件
  • 农特产品如何做网站品牌营销策划案例ppt
  • 成都电子商城网站开发目前最流行的拓客方法
  • 广州网站站建设培训网络推广公司方案
  • 个人备案网站做淘宝客可以百度学术论文查重入口
  • 做动图为所欲为的网站百度搜索量怎么查
  • 政府门户网站建设相关资料廊坊seo外包
  • 兰州网站怎么建设百度快照入口
  • 做暧暖网站无锡百度推广代理商
  • 设计开发上海网站设计开发公司网站群发软件
  • 建设的网站首页黄冈网站推广软件
  • 万网有网站建设吗排名轻松seo 网站
  • 做网站需要注意的点优化关键词排名优化公司
  • 服饰东莞网站建设网络公司seo推广
  • 施工企业向建设单位提供预付款担保产生的费用属于优化推广方案
  • wordpress 双栏目百度seo工具
  • 个人网站html模板衡阳网站建设