政务公开和网站建设情况百度的竞价排名是哪种方式
文章目录
- 1、Curve Fitting
- 1.1、残差定义
- 1.2、 Problem问题构造
- 1.3、完整代码
- 1.4、运行结果
- 2、Robust Curve Fitting
1、Curve Fitting
到目前为止,我们看到的示例都是没有数据的简单优化问题。最小二乘和非线性最小二乘分析的原始目的是对数据进行曲线拟合。
以一个简单的曲线拟合的问题为例。采样点是根据曲线 y=e0.3x+0.1y = e^{0.3x + 0.1}y=e0.3x+0.1 生成,并且添加标准差 σ=0.2σ=0.2σ=0.2 的高斯噪声。我们用下列带未知参数的方程来拟合这些采样点:y=emx+c.y = e^{mx + c}.y=emx+c.
1.1、残差定义
首先定义一个模板对象来计算残差。每一个观察值(采样点)都有一个残差,
struct ExponentialResidual {ExponentialResidual(double x, double y): x_(x), y_(y) {}template <typename T>bool operator()(const T* const m, const T* const c, T* residual) const {residual[0] = y_ - exp(m[0] * x_ + c[0]);return true;}private:// Observations for a sample.const double x_;const double y_;
};
1.2、 Problem问题构造
假设观测数据是一个名为data的2n大小的的数组,为每一个观察值创建一个CostFunction的问题(problem)构造是一个简单的事。
double m = 0.0;
double c = 0.0;Problem problem;
for (int i = 0; i < kNumObservations; ++i) {CostFunction* cost_function =new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(new ExponentialResidual(data[2 * i], data[2 * i + 1]));problem.AddResidualBlock(cost_function, nullptr, &m, &c);
}
*/
与Hello World的f(x)=10−x对比:
struct CostFunctor {template <typename T>bool operator()(const T* const x, T* residual) const {residual[0] = T(10.0) - x[0];return true;}
};
CostFunction* cost_function =new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
problem.AddResidualBlock(cost_function, NULL, &x);
对比结果:
- 1.在Hello World中,CostFunctor中是没有(显式)构造函数的,也就同样没有了初始值。所以在构造对象时,可以直接New CostFunctor。而在本节的例子中,构造对象时还要加上初始值,即
new ExponentialResidual(data[2 * i], data[2 * i + 1])); - 2.在AutoDiffCostFunction的模板中,本例中一共有三个1,而在Hello World中,只有两个1,即residual和x的维度。注意先是残差,后是输入参数,而且一一对应。
1.3、完整代码
// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
// this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
// this list of conditions and the following disclaimer in the documentation
// and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
// used to endorse or promote products derived from this software without
// specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: sameeragarwal@google.com (Sameer Agarwal)#include "ceres/ceres.h"
#include "glog/logging.h"using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;// Data generated using the following octave code.
// randn('seed', 23497);
// m = 0.3;
// c = 0.1;
// x=[0:0.075:5];
// y = exp(m * x + c);
// noise = randn(size(x)) * 0.2;
// y_observed = y + noise;
// data = [x', y_observed'];const int kNumObservations = 67;
const double data[] = {0.000000e+00, 1.133898e+00,7.500000e-02, 1.334902e+00,1.500000e-01, 1.213546e+00,2.250000e-01, 1.252016e+00,3.000000e-01, 1.392265e+00,3.750000e-01, 1.314458e+00,4.500000e-01, 1.472541e+00,5.250000e-01, 1.536218e+00,6.000000e-01, 1.355679e+00,6.750000e-01, 1.463566e+00,7.500000e-01, 1.490201e+00,8.250000e-01, 1.658699e+00,9.000000e-01, 1.067574e+00,9.750000e-01, 1.464629e+00,1.050000e+00, 1.402653e+00,1.125000e+00, 1.713141e+00,1.200000e+00, 1.527021e+00,1.275000e+00, 1.702632e+00,1.350000e+00, 1.423899e+00,1.425000e+00, 1.543078e+00,1.500000e+00, 1.664015e+00,1.575000e+00, 1.732484e+00,1.650000e+00, 1.543296e+00,1.725000e+00, 1.959523e+00,1.800000e+00, 1.685132e+00,1.875000e+00, 1.951791e+00,1.950000e+00, 2.095346e+00,2.025000e+00, 2.361460e+00,2.100000e+00, 2.169119e+00,2.175000e+00, 2.061745e+00,2.250000e+00, 2.178641e+00,2.325000e+00, 2.104346e+00,2.400000e+00, 2.584470e+00,2.475000e+00, 1.914158e+00,2.550000e+00, 2.368375e+00,2.625000e+00, 2.686125e+00,2.700000e+00, 2.712395e+00,2.775000e+00, 2.499511e+00,2.850000e+00, 2.558897e+00,2.925000e+00, 2.309154e+00,3.000000e+00, 2.869503e+00,3.075000e+00, 3.116645e+00,3.150000e+00, 3.094907e+00,3.225000e+00, 2.471759e+00,3.300000e+00, 3.017131e+00,3.375000e+00, 3.232381e+00,3.450000e+00, 2.944596e+00,3.525000e+00, 3.385343e+00,3.600000e+00, 3.199826e+00,3.675000e+00, 3.423039e+00,3.750000e+00, 3.621552e+00,3.825000e+00, 3.559255e+00,3.900000e+00, 3.530713e+00,3.975000e+00, 3.561766e+00,4.050000e+00, 3.544574e+00,4.125000e+00, 3.867945e+00,4.200000e+00, 4.049776e+00,4.275000e+00, 3.885601e+00,4.350000e+00, 4.110505e+00,4.425000e+00, 4.345320e+00,4.500000e+00, 4.161241e+00,4.575000e+00, 4.363407e+00,4.650000e+00, 4.161576e+00,4.725000e+00, 4.619728e+00,4.800000e+00, 4.737410e+00,4.875000e+00, 4.727863e+00,4.950000e+00, 4.669206e+00,
};struct ExponentialResidual {ExponentialResidual(double x, double y): x_(x), y_(y) {}template <typename T> bool operator()(const T* const m,const T* const c,T* residual) const {residual[0] = y_ - exp(m[0] * x_ + c[0]);return true;}private:const double x_;const double y_;
};int main(int argc, char** argv) {google::InitGoogleLogging(argv[0]);double m = 0.0;double c = 0.0;Problem problem;for (int i = 0; i < kNumObservations; ++i) {problem.AddResidualBlock(new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(new ExponentialResidual(data[2 * i], data[2 * i + 1])),NULL,&m, &c);}Solver::Options options;options.max_num_iterations = 25;options.linear_solver_type = ceres::DENSE_QR;options.minimizer_progress_to_stdout = true;Solver::Summary summary;Solve(options, &problem, &summary);std::cout << summary.BriefReport() << "\n";std::cout << "Initial m: " << 0.0 << " c: " << 0.0 << "\n";std::cout << "Final m: " << m << " c: " << c << "\n";return 0;
}
1.4、运行结果
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time0 1.211734e+02 0.00e+00 3.61e+02 0.00e+00 0.00e+00 1.00e+04 0 1.84e-03 2.30e-031 2.334822e+03 -2.21e+03 0.00e+00 7.52e-01 -1.87e+01 5.00e+03 1 7.51e-04 3.41e-032 2.331438e+03 -2.21e+03 0.00e+00 7.51e-01 -1.86e+01 1.25e+03 1 3.35e-04 3.82e-033 2.311313e+03 -2.19e+03 0.00e+00 7.48e-01 -1.85e+01 1.56e+02 1 3.31e-04 4.22e-034 2.137268e+03 -2.02e+03 0.00e+00 7.22e-01 -1.70e+01 9.77e+00 1 3.32e-04 4.62e-035 8.553131e+02 -7.34e+02 0.00e+00 5.78e-01 -6.32e+00 3.05e-01 1 3.30e-04 5.02e-036 3.306595e+01 8.81e+01 4.10e+02 3.18e-01 1.37e+00 9.16e-01 1 1.95e-03 7.04e-037 6.426770e+00 2.66e+01 1.81e+02 1.29e-01 1.10e+00 2.75e+00 1 2.03e-03 9.14e-038 3.344546e+00 3.08e+00 5.51e+01 3.05e-02 1.03e+00 8.24e+00 1 4.12e-03 1.34e-029 1.987485e+00 1.36e+00 2.33e+01 8.87e-02 9.94e-01 2.47e+01 1 2.04e-03 1.55e-0210 1.211585e+00 7.76e-01 8.22e+00 1.05e-01 9.89e-01 7.42e+01 1 1.96e-03 1.76e-0211 1.063265e+00 1.48e-01 1.44e+00 6.06e-02 9.97e-01 2.22e+02 1 1.97e-03 1.96e-0212 1.056795e+00 6.47e-03 1.18e-01 1.47e-02 1.00e+00 6.67e+02 1 1.97e-03 2.17e-0213 1.056751e+00 4.39e-05 3.79e-03 1.28e-03 1.00e+00 2.00e+03 1 1.96e-03 2.40e-02
Ceres Solver Report: Iterations: 14, Initial cost: 1.211734e+02, Final cost: 1.056751e+00, Termination: CONVERGENCE
Initial m: 0 c: 0
Final m: 0.291861 c: 0.131439
参数的初始值为m=0,c=0,初始代价函数为121.173。最后的解是m=0.291861,c=0.131439,代价是1.05675。
这个结果和期望解m=0.3,c=0.1有一些细微的差别,但是是合理的(因为添加了高斯噪声)。当从噪声数据重建曲线时,我们预计会看到这样的偏差。
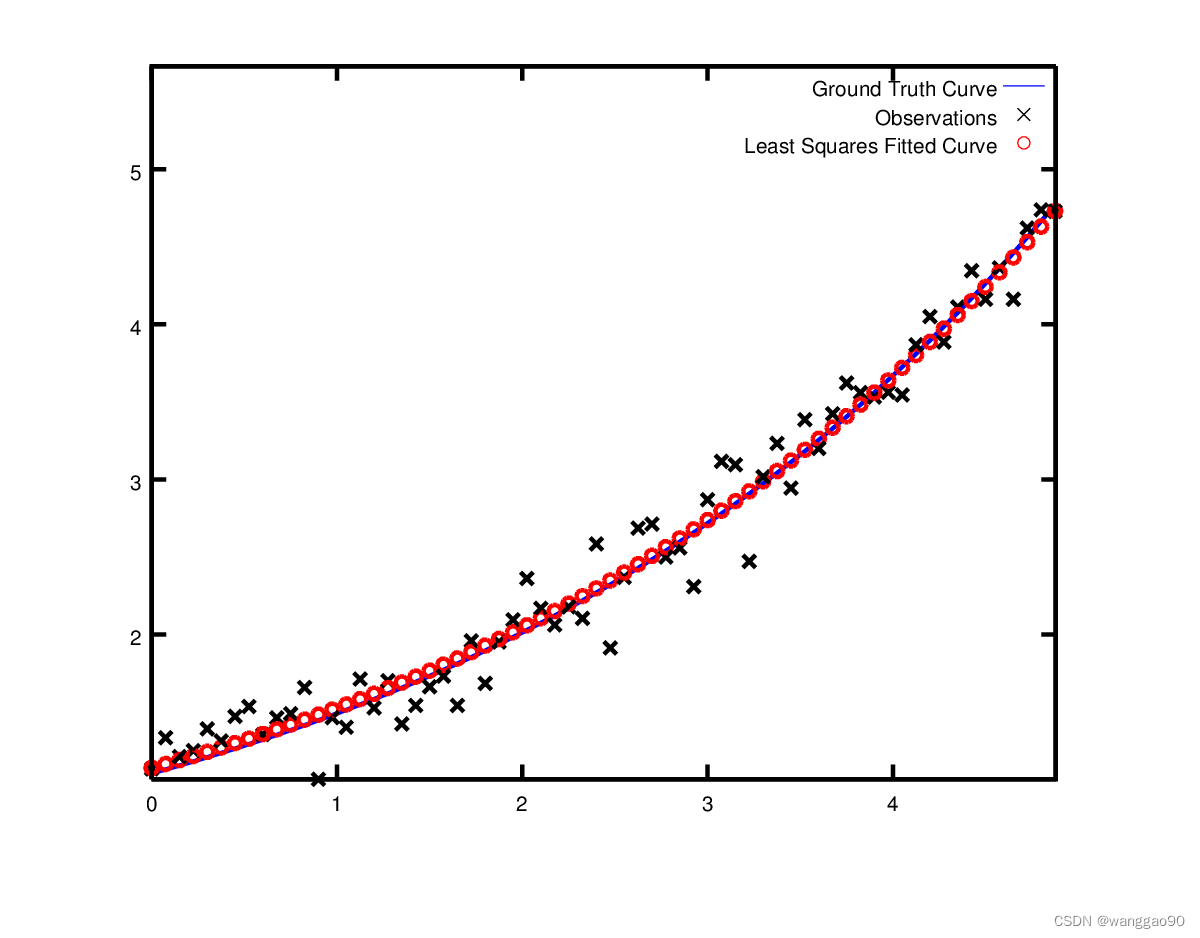
实际上,如果您要对m=0.3,c=0.1的目标函数进行评估,那么当目标函数值为1.082425时,拟合效果会更差。下图说明了适合度。
2、Robust Curve Fitting
现在假设我们给出的数据有一些异常值(离群点/外点),也就是说,我们有一些点不服从噪声模型,继续使用上面的代码来拟合这些数据,我们将得到拟合曲线是偏离实际预期。
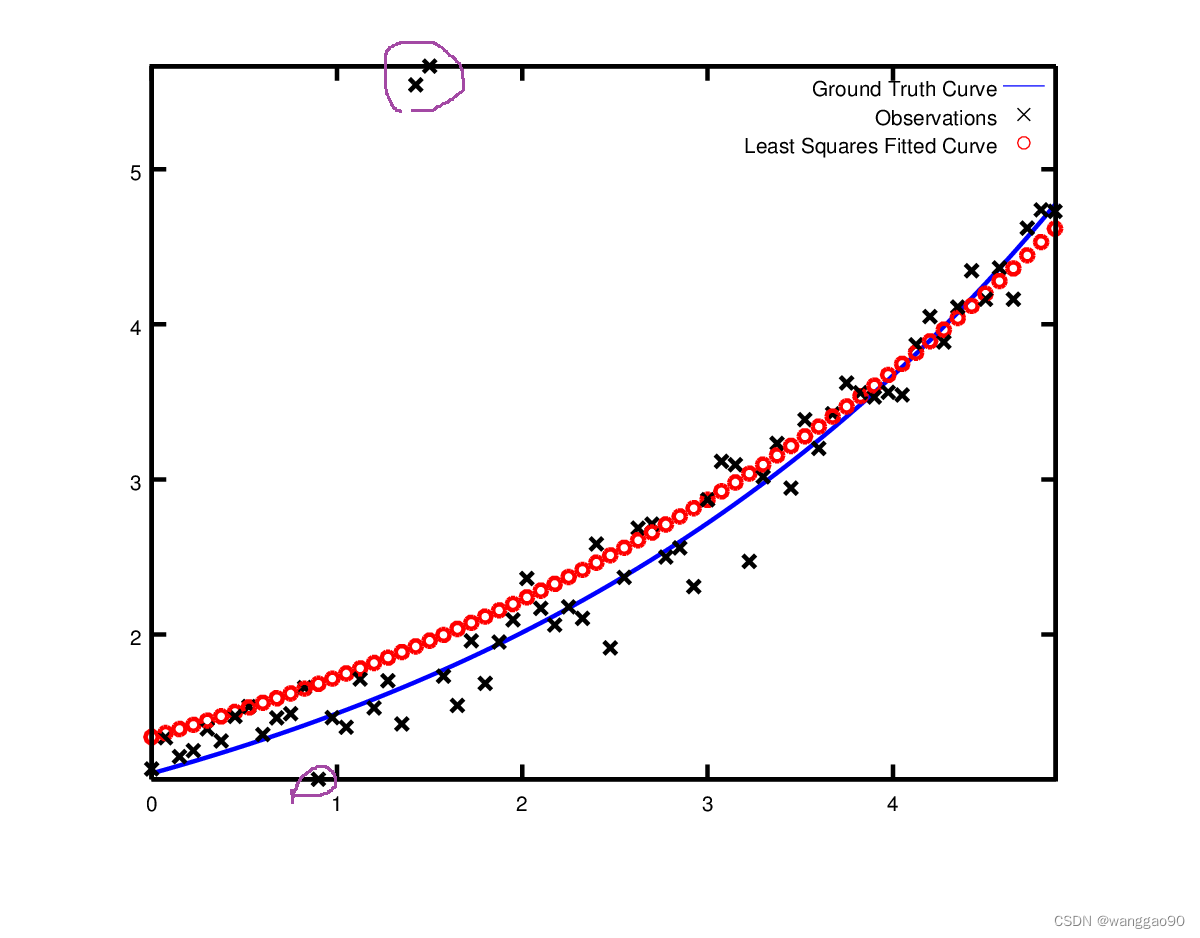
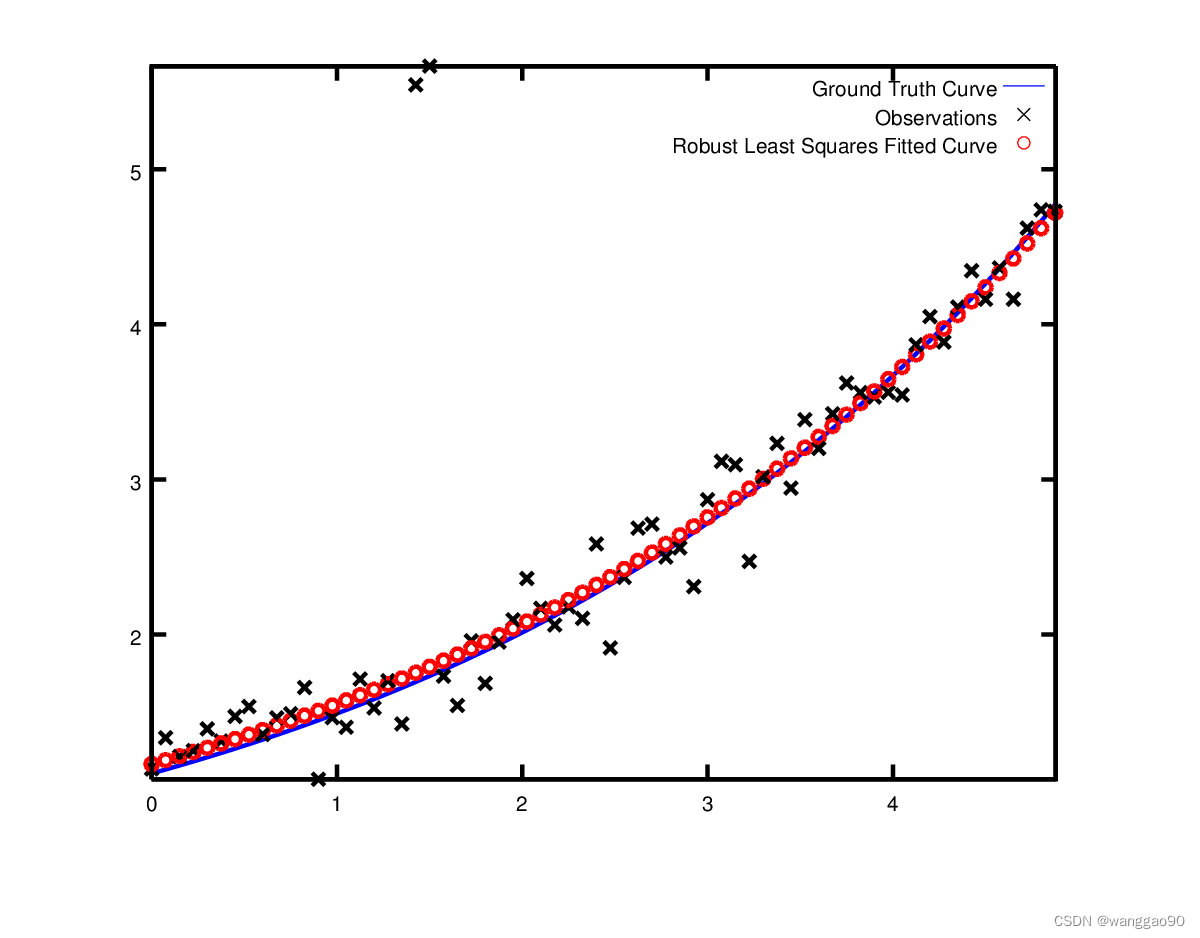
处理异常值的标准方法是使用LossFunction。损失函数降低了残差高的残差块(通常是与异常值对应的残差块)的影响。为了将损失函数与残差块联系起来,我们改变
// problem.AddResidualBlock(cost_function, nullptr , &m, &c);problem.AddResidualBlock(cost_function, new CauchyLoss(0.5) , &m, &c);
这里使用SizedCostFunction类,需要填写计算jacobians。完整代码如下
#include "ceres/ceres.h"
#include "glog/logging.h"// Data generated using the following octave code.
// randn('seed', 23497);
// m = 0.3;
// c = 0.1;
// x=[0:0.075:5];
// y = exp(m * x + c);
// noise = randn(size(x)) * 0.2;
// outlier_noise = rand(size(x)) < 0.05;
// y_observed = y + noise + outlier_noise;
// data = [x', y_observed'];const int kNumObservations = 67;
const double data[] = {
0.000000e+00, 1.133898e+00,
7.500000e-02, 1.334902e+00,
1.500000e-01, 1.213546e+00,
2.250000e-01, 1.252016e+00,
3.000000e-01, 1.392265e+00,
3.750000e-01, 1.314458e+00,
4.500000e-01, 1.472541e+00,
5.250000e-01, 1.536218e+00,
6.000000e-01, 1.355679e+00,
6.750000e-01, 1.463566e+00,
7.500000e-01, 1.490201e+00,
8.250000e-01, 1.658699e+00,
9.000000e-01, 1.067574e+00,
9.750000e-01, 1.464629e+00,
1.050000e+00, 1.402653e+00,
1.125000e+00, 1.713141e+00,
1.200000e+00, 1.527021e+00,
1.275000e+00, 1.702632e+00,
1.350000e+00, 1.423899e+00,
1.425000e+00, 5.543078e+00, // Outlier point
1.500000e+00, 5.664015e+00, // Outlier point
1.575000e+00, 1.732484e+00,
1.650000e+00, 1.543296e+00,
1.725000e+00, 1.959523e+00,
1.800000e+00, 1.685132e+00,
1.875000e+00, 1.951791e+00,
1.950000e+00, 2.095346e+00,
2.025000e+00, 2.361460e+00,
2.100000e+00, 2.169119e+00,
2.175000e+00, 2.061745e+00,
2.250000e+00, 2.178641e+00,
2.325000e+00, 2.104346e+00,
2.400000e+00, 2.584470e+00,
2.475000e+00, 1.914158e+00,
2.550000e+00, 2.368375e+00,
2.625000e+00, 2.686125e+00,
2.700000e+00, 2.712395e+00,
2.775000e+00, 2.499511e+00,
2.850000e+00, 2.558897e+00,
2.925000e+00, 2.309154e+00,
3.000000e+00, 2.869503e+00,
3.075000e+00, 3.116645e+00,
3.150000e+00, 3.094907e+00,
3.225000e+00, 2.471759e+00,
3.300000e+00, 3.017131e+00,
3.375000e+00, 3.232381e+00,
3.450000e+00, 2.944596e+00,
3.525000e+00, 3.385343e+00,
3.600000e+00, 3.199826e+00,
3.675000e+00, 3.423039e+00,
3.750000e+00, 3.621552e+00,
3.825000e+00, 3.559255e+00,
3.900000e+00, 3.530713e+00,
3.975000e+00, 3.561766e+00,
4.050000e+00, 3.544574e+00,
4.125000e+00, 3.867945e+00,
4.200000e+00, 4.049776e+00,
4.275000e+00, 3.885601e+00,
4.350000e+00, 4.110505e+00,
4.425000e+00, 4.345320e+00,
4.500000e+00, 4.161241e+00,
4.575000e+00, 4.363407e+00,
4.650000e+00, 4.161576e+00,
4.725000e+00, 4.619728e+00,
4.800000e+00, 4.737410e+00,
4.875000e+00, 4.727863e+00,
4.950000e+00, 4.669206e+00
};using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::CauchyLoss;
using ceres::Problem;
using ceres::Solve;
using ceres::Solver;class ExponentialResidual : public ceres::SizedCostFunction<1, 2> {
public:ExponentialResidual(double x, double y): x_(x), y_(y) { }virtual bool Evaluate(const double* const* mc,double* residual,double** jacobians) const override{double tmp_y = exp(mc[0][0] * x_ + mc[0][1]);residual[0] = tmp_y - y_; // r = exp(mx+c) - y if(jacobians && jacobians[0]) {jacobians[0][0] = x_ * tmp_y; // dr / dmjacobians[0][1] = tmp_y; // dr / dc}return true;}private:const double x_, y_;
};int main(int argc, char** argv) {google::InitGoogleLogging(argv[0]);double mc[] = {0,0};double &m = mc[0];double &c = mc[1];Problem problem;for (int i = 0; i < kNumObservations; ++i) {problem.AddResidualBlock(new ExponentialResidual(data[2 * i], data[2 * i + 1]),new CauchyLoss(0.5), // 使用损失LossFunction,不再是nullptrmc);}Solver::Options options;options.linear_solver_type = ceres::DENSE_QR;options.minimizer_progress_to_stdout = true;Solver::Summary summary;Solve(options, &problem, &summary);std::cout << summary.BriefReport() << "\n";std::cout << "Initial m: " << 0.0 << " c: " << 0.0 << "\n";std::cout << "Final m: " << m << " c: " << c << "\n";return 0;
}
CauchyLoss 是Ceres Solver中的一个损失函数,参数0.5指定了损失函数的尺度。重新运行程序,得到的优化的结果相比不使用损失函数的结果更优。
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time0 1.815138e+01 0.00e+00 2.04e+01 0.00e+00 0.00e+00 1.00e+04 0 6.93e-04 1.14e-031 2.259471e+01 -4.44e+00 0.00e+00 5.48e-01 -7.74e-01 5.00e+03 1 7.61e-04 2.26e-032 2.258929e+01 -4.44e+00 0.00e+00 5.48e-01 -7.73e-01 1.25e+03 1 4.05e-04 2.74e-033 2.255683e+01 -4.41e+00 0.00e+00 5.48e-01 -7.68e-01 1.56e+02 1 4.51e-04 5.16e-034 2.225747e+01 -4.11e+00 0.00e+00 5.41e-01 -7.16e-01 9.77e+00 1 3.37e-04 5.58e-035 1.784270e+01 3.09e-01 8.54e+01 4.72e-01 5.44e-02 5.72e+00 1 8.33e-04 6.48e-036 7.557353e+00 1.03e+01 1.13e+02 1.06e-01 2.07e+00 1.72e+01 1 8.29e-04 7.38e-037 2.674796e+00 4.88e+00 7.69e+01 5.41e-02 1.78e+00 5.15e+01 1 8.22e-04 8.28e-038 1.946177e+00 7.29e-01 1.61e+01 5.00e-02 1.23e+00 1.54e+02 1 8.22e-04 9.17e-039 1.904587e+00 4.16e-02 2.20e+00 2.64e-02 1.11e+00 4.63e+02 1 8.23e-04 1.01e-0210 1.902929e+00 1.66e-03 2.28e-01 6.94e-03 1.12e+00 1.39e+03 1 8.93e-04 1.10e-0211 1.902884e+00 4.51e-05 1.49e-02 1.27e-03 1.14e+00 4.17e+03 1 9.34e-04 1.21e-02
Ceres Solver Report: Iterations: 12, Initial cost: 1.815138e+01, Final cost: 1.902884e+00, Termination: CONVERGENCE
Initial m: 0 c: 0
Final m: 0.287605 c: 0.151213