影视网站建设营销方式和手段

✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。
🍎个人主页：小嗷犬的个人主页
🍊个人网站：小嗷犬的技术小站
🥭个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。

---

---

引入

图论中的树和现实生活中的树长得一样，只不过我们习惯于处理问题的时候把树根放到上方来考虑。

这种数据结构看起来像是一个倒挂的树，因此得名。

---

定义

一个没有固定根结点的树称为 无根树（unrooted tree）。无根树有几种等价的形式化定义：

• 有 $n$ 个结点，$n-1$ 条边的连通无向图
• 无向无环的连通图
• 任意两个结点之间有且仅有一条简单路径的无向图
• 任何边均为桥的连通图
• 没有圈，且在任意不同两点间添加一条边之后所得图含唯一的一个圈的图

在无根树的基础上，指定一个结点称为 根，则形成一棵 有根树（rooted tree）。有根树在很多时候仍以无向图表示，只是规定了结点之间的上下级关系，详见下文。

---

有关树的定义

适用于无根树和有根树

• 森林（forest）：每个连通分量（连通块）都是树的图。按照定义，一棵树也是森林。
• 生成树（spanning tree）：一个连通无向图的生成子图，同时要求是树。也即在图的边集中选择 $n-1$ 条，将所有顶点连通。
• 无根树的叶结点（leaf node）：度数不超过 $1$ 的结点。
• 有根树的叶结点（leaf node）：没有子结点的结点。

只适用于有根树

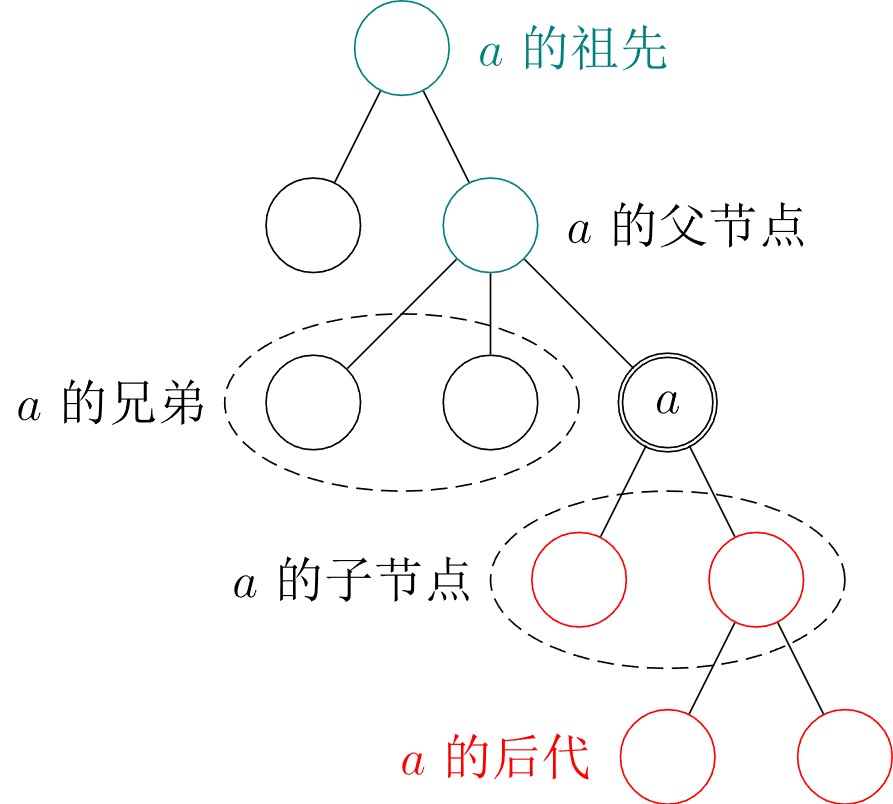
• 父亲（parent node）：对于除根以外的每个结点，定义为从该结点到根路径上的第二个结点。 根结点没有父结点。

• 祖先（ancestor）：一个结点到根结点的路径上，除了它本身外的结点。 根结点的祖先集合为空。

• 子结点（child node）：如果 $u$ 是 $v$ 的父亲，那么 $v$ 是 $u$ 的子结点。
  子结点的顺序一般不加以区分，二叉树是一个例外。

• 结点的深度（depth）：到根结点的路径上的边数。

• 树的高度（height）：所有结点的深度的最大值。

• 兄弟（sibling）：同一个父亲的多个子结点互为兄弟。

• 后代（descendant）：子结点和子结点的后代。
  或者理解成：如果 $u$ 是 $v$ 的祖先，那么 $v$ 是 $u$ 的后代。
  

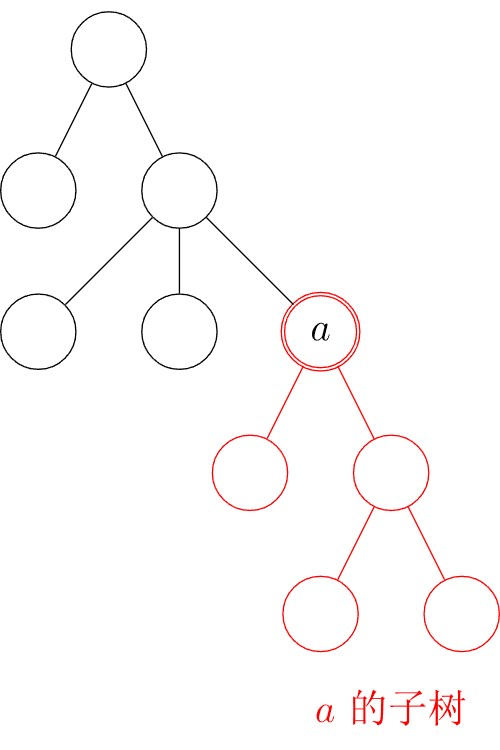
• 子树（subtree）：删掉与父亲相连的边后，该结点所在的子图。
  

---

特殊的树

• 链（chain/path graph）：满足与任一结点相连的边不超过 $2$ 条的树称为链。

• 菊花/星星（star）：满足存在 $u$ 使得所有除 $u$ 以外结点均与 $u$ 相连的树称为菊花。

• 有根二叉树（rooted binary tree）：每个结点最多只有两个儿子（子结点）的有根树称为二叉树。常常对两个子结点的顺序加以区分，分别称之为左子结点和右子结点。
  大多数情况下，二叉树 一词均指有根二叉树。

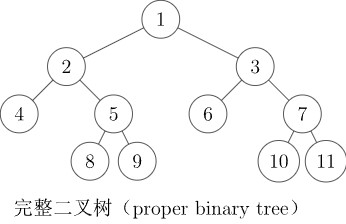
• 完整二叉树（full/proper binary tree）：每个结点的子结点数量均为 $0$ 或者 $2$ 的二叉树。换言之，每个结点或者是树叶，或者左右子树均非空。
  

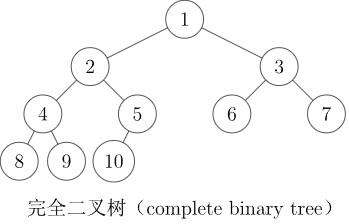
• 完全二叉树（complete binary tree）：只有最下面两层结点的度数可以小于 $2$，且最下面一层的结点都集中在该层最左边的连续位置上。
  

• 完美二叉树（perfect binary tree）：所有叶结点的深度均相同的二叉树称为完美二叉树。
  

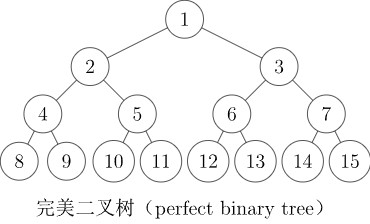
Proper binary tree 的汉译名称不固定，且完全二叉树和满二叉树的定义在不同教材中定义不同，遇到的时候需根据上下文加以判断。

ACMer 所说的「满二叉树」多指完美二叉树。

---

存储

只记录父结点

用一个数组 parent[N] 记录每个结点的父亲结点。

这种方式可以获得的信息较少，不便于进行自顶向下的遍历。常用于自底向上的递推问题中。

邻接表

• 对于无根树：为每个结点开辟一个线性列表，记录所有与之相连的结点。

  std::vector<int> adj[N];
  

• 对于有根树：

  • 方法一：若给定的是无向图，则仍可以上述形式存储。下文将介绍如何区分结点的上下关系。

  • 方法二：若输入数据能够确保结点的上下关系，则可以利用这个信息。为每个结点开辟一个线性列表，记录其所有子结点；若有需要，还可在另一个数组中记录其父结点。

    std::vector<int> children[N];
    int parent[N];
    

    当然也可以用其他方式（如链表）替代 std::vector。

左孩子右兄弟表示法

过程

对于有根树，存在一种简单的表示方法。

首先，给每个结点的所有子结点任意确定一个顺序。

此后为每个结点记录两个值：其 第一个子结点 child[u] 和其 下一个兄弟结点 sib[u]。若没有子结点，则 child[u] 为空；若该结点是其父结点的最后一个子结点，则 sib[u] 为空。

实现

遍历一个结点的所有子结点可由如下方式实现。

int v = child[u]; // 从第一个子结点开始
while (v != EMPTY_NODE)
{// ...// 处理子结点 v// ...v = sib[v]; // 转至下一个子结点，即 v 的一个兄弟
}

也可简写为以下形式。

for (int v = child[u]; v != EMPTY_NODE; v = sib[v])
{// ...// 处理子结点 v// ...
}

二叉树

需要记录每个结点的左右子结点。

int parent[N];
int lch[N], rch[N];
// -- or --
int child[N][2];

---

树的遍历

树上 DFS

在树上 DFS 是这样的一个过程：先访问根节点，然后分别访问根节点每个儿子的子树。

可以用来求出每个节点的深度、父亲等信息。

二叉树上 DFS

前序遍历

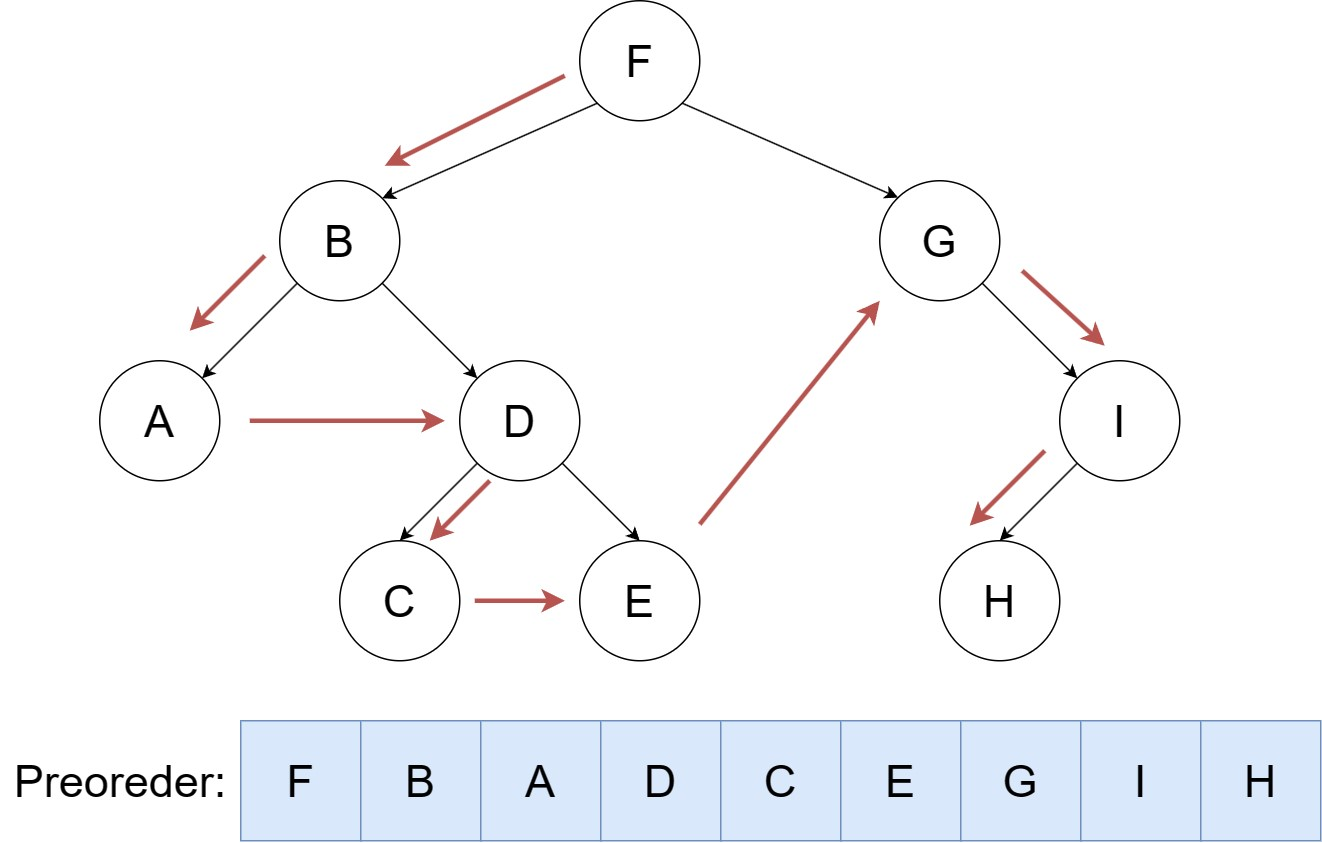
按照 根，左，右 的顺序遍历二叉树。

void preTrav(BiTree *root)
{if (root){cout << root->key << " ";preTrav(root->left);preTrav(root->right);}
}

中序遍历

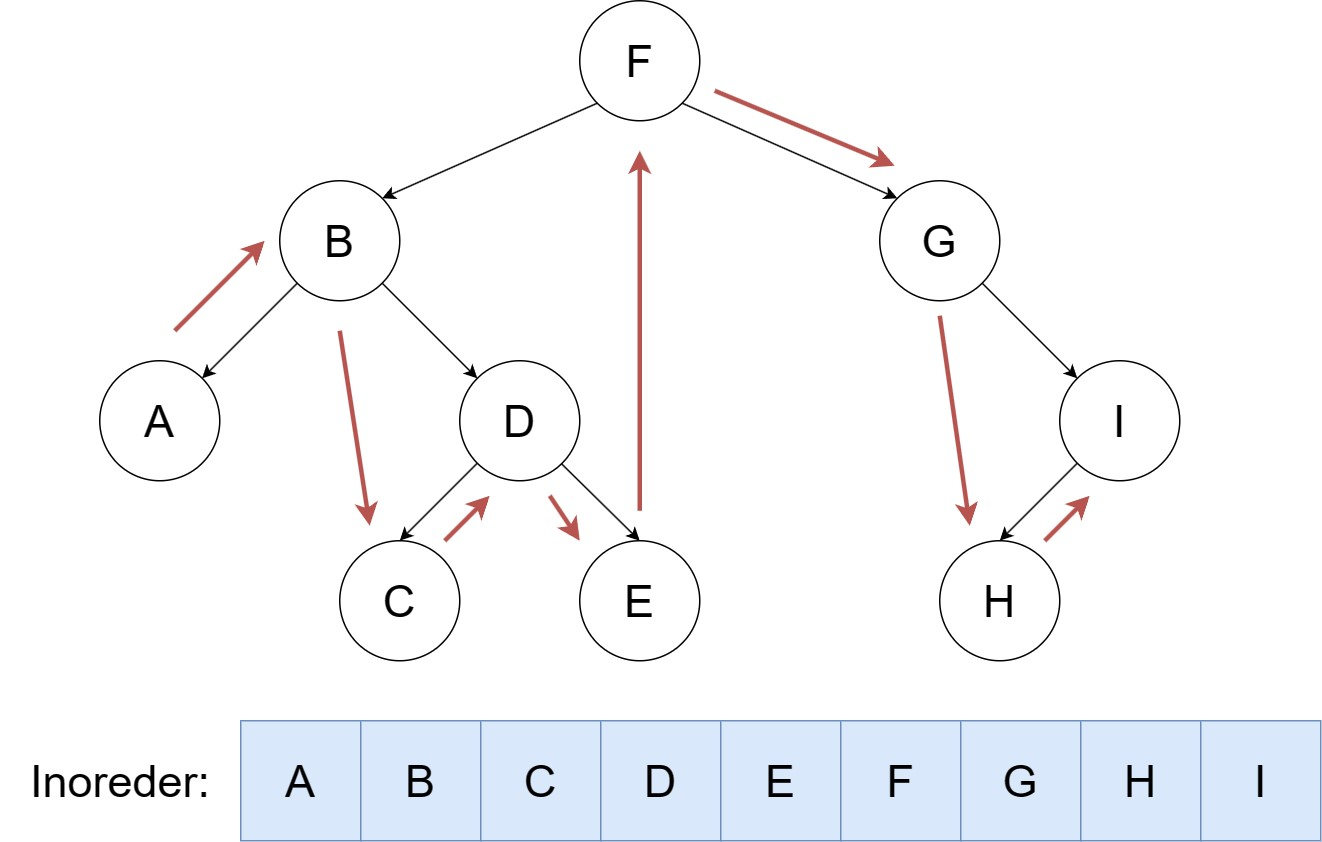
按照 左，根，右 的顺序遍历二叉树。

void midTrav(BiTree *root)
{if (root){midTrav(root->left);cout << root->key << " ";midTrav(root->right);}
}

后序遍历

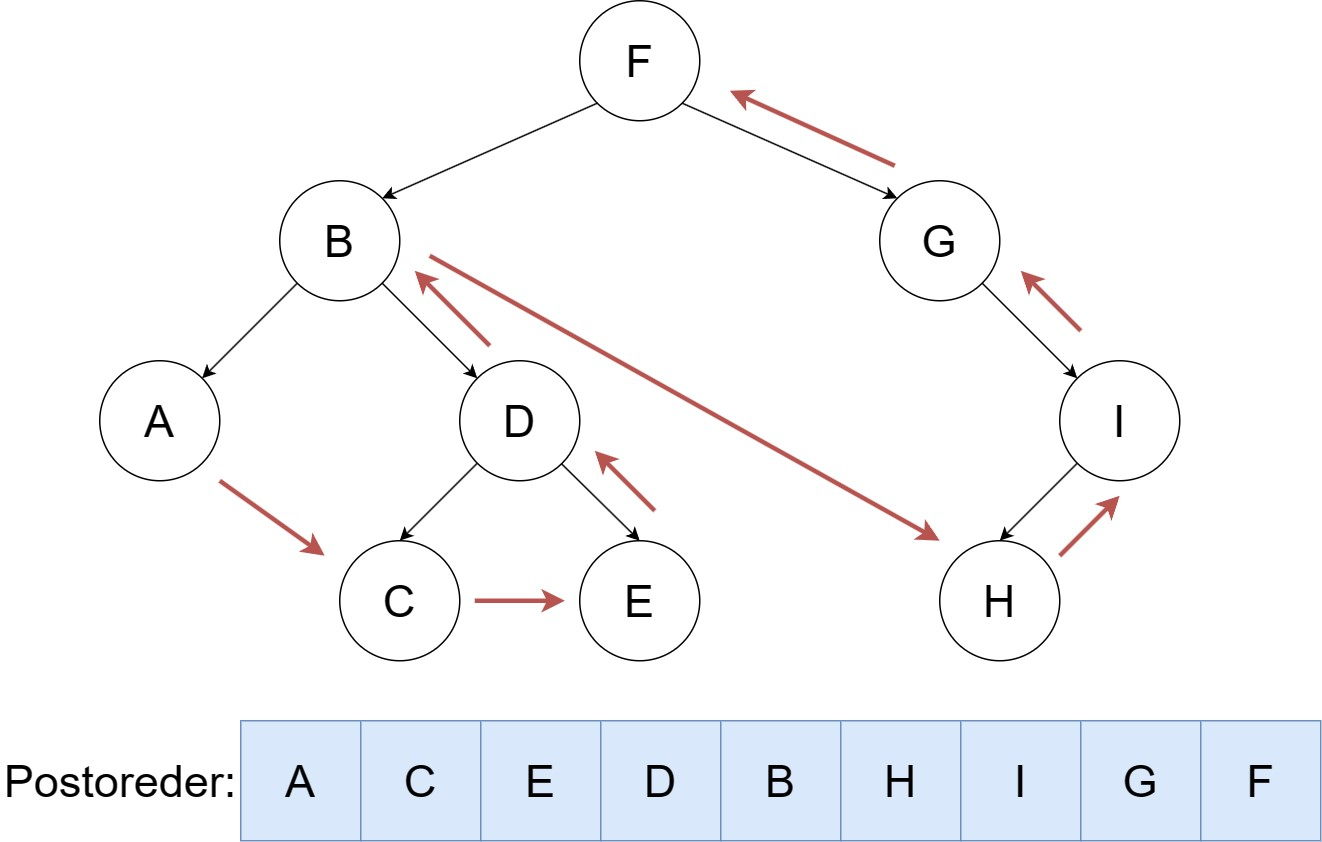
按照 左，右，根 的顺序遍历二叉树。

void lastTrav(BiTree *root)
{if (root){lastTrav(root->left);lastTrav(root->right);cout << root->key << " ";}
}

反推

已知中序遍历序列和另外一个序列可以求第三个序列。

1. 前序的第一个是 root，后序的最后一个是 root。
2. 先确定根节点，然后根据中序遍历，在根左边的为左子树，根右边的为右子树。
3. 对于每一个子树可以看成一个全新的树，仍然遵循上面的规律。

树上 BFS

从树根开始，严格按照层次来访问节点。

BFS 过程中也可以顺便求出各个节点的深度和父亲节点。

无根树

过程

树的遍历一般为深度优先遍历，这个过程中最需要注意的是避免重复访问结点。

由于树是无环图，因此只需记录当前结点是由哪个结点访问而来，此后进入除该结点外的所有相邻结点，即可避免重复访问。

实现

void dfs(int u, int from)
{// 递归进入除了 from 之外的所有子结点// 对于出发结点，from 为空，故会访问所有相邻结点，这与期望一致for (int v : adj[u])if (v != from)dfs(v, u);
}// 开始遍历时
int EMPTY_NODE = -1; // 一个不存在的编号
int root = 0;        // 任取一个结点作为出发点
dfs(root, EMPTY_NODE);

有根树

对于有根树，需要区分结点的上下关系。

考察上面的遍历过程，若从根开始遍历，则访问到一个结点时 from 的值，就是其父结点的编号。

通过这个方式，可以对于无向的输入求出所有结点的父结点，以及子结点列表。