红黑树

一、红黑树的概念

红黑树（Red Black Tree） 是一种自平衡二叉查找树，在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

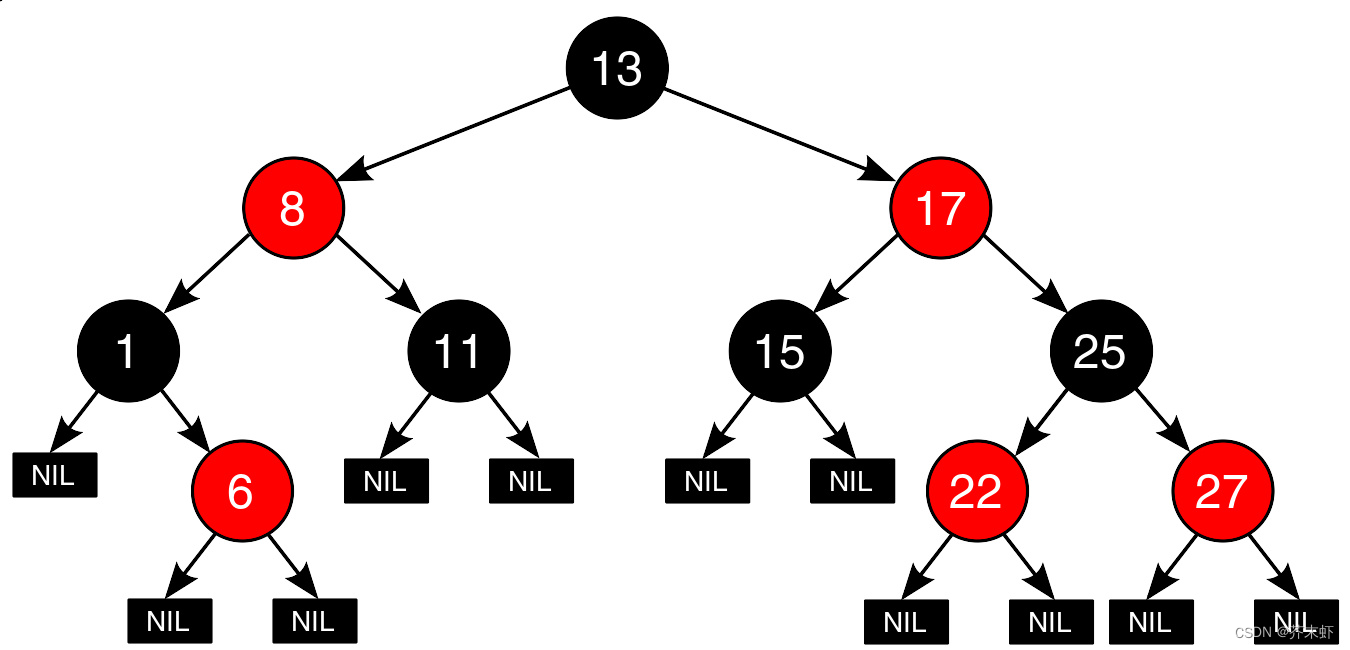
AVL树 VS 红黑树

• 红黑树是一种特化的AVL树，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

• AVL树要求每棵子树的左右高度差不超过1，是严格平衡；而红黑树要求最长路径不超过最短路径的2倍，是接近平衡。

• 而红黑树是一种AVL树的变体，它要求最长路径不超过最短路径的2倍，左右子树高差有可能大于 1。所以红黑树不是严格意义上的平衡二叉树（AVL），但对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。

• 相对而言，插入或删除同样的数据，AVL树旋转的更多，而红黑树则旋转的更少效率相对较高。

---

二、红黑树的性质

红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。 在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

• 性质1. 结点是红色或黑色。

• 性质2. 根结点是黑色。

• 性质3. 每个红色结点的两个子结点都是黑色。（每条路径上不能有两个连续的红色结点）

• 性质4. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。 （每条路径上的黑色节点数量相同）

• 性质5. 所有NIL结点都是黑色的。（NIL节点即空结点）

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

是性质3导致路径上不能有两个连续的红色结点确保了这个结果。最短的可能路径都是黑色结点，最长的可能路径有交替的红色和黑色结点。因为根据性质4所有路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。

思考：新插入的节点应该设为黑色还是红色？

• 如果将新插入的节点设为黑色，不管插到那条路径都必然违反性质4。

• 如果将新插入的节点设为红色：如果父节点是红色则违反性质3，需要进行调整；如果父节点是黑色就正常插入，无需调整。

• 对比两种情况，最终选择将新插入的节点设为红色。

---

三、STL中的红黑树结构

• 为了后续实现关联式容器map/set，STL红黑树的实现中增加一个头结点；
• 因为根节点必须为黑色，为了与根节点进行区分，将头结点给成红色；
• 并且让头结点的_parent域指向红黑树的根节点，_left域指向红黑树中最小的节点，_right域指向红黑树中最大的节点。

头结点的作用：

• STL明确规定，begin()与end()代表的是一段前闭后开的区间，而对红黑树进行中序遍历后，可以得到一个有序的序列，因此：begin()可以放在红黑树中最小节点(即最左侧节点)的位置，end()放在最大节点(最右侧节点)的下一个位置，关键是最大节点的下一个位置在哪块？
• 能否给成nullptr呢？答案是行不通的，因为对end()位置的迭代器进行–操作，必须要能找最后一个元素，此处就不行，因此最好的方式是将end()放在头结点的位置：

---

四、核心结构

enum Color{RED,BLACK
};
//红黑树的节点
template <class K, class V>
struct RBTreeNode{ RBTreeNode<K,V> *_left;RBTreeNode<K,V> *_right;RBTreeNode<K,V> *_parent;pair<K,V> _kv;Color _color; //颜色属性RBTreeNode(const pair<K,V> &kv=pair<K,V>(), Color color = RED):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_color(color){}
};//红黑树结构
template <class K, class V>
class RBTree{ typedef RBTreeNode<K,V> Node;Node *_phead; //指向头结点的指针public:RBTree(){_phead = new Node; //红黑树的头结点_phead->_left = _phead; //起初先让头结点的左右指针指向自己_phead->_right = _phead;}Node*& GetRoot(){ //返回根节点指针的引用，便于进行修改return _phead->_parent; }//........
private:Node* LeftMost(){ //返回红黑树的最左节点指针Node *root = GetRoot();if(root == nullptr) //如果根节点为空，就返回_pheadreturn _phead;else{Node *left = root;while(left->_left!=nullptr){left = left->_left;}return left;}}Node* RightMost(){ //返回红黑树的最右节点指针Node *root = GetRoot();if(root == nullptr) //如果根节点为空，就返回_pheadreturn _phead;else{Node *right = root;while(right->_right!=nullptr){right = right->_right;}return right;}}//......
};

---

五、红黑树的插入操作

红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此红黑树的插入可分为两步：

1. 按照二叉搜索的树规则插入新节点

2. 检测新节点插入后，红黑树的性质是否造到破坏。因为新节点的默认颜色是红色，因此：

   • 如果新插入的节点是根节点，需要将节点变为黑色以满足性质2。
   • 如果父节点是黑色的，没有违反红黑树的任何性质，则不需要调整；
   • 但如果父节点颜色为红色时，就违反了性质3：路径上不能有两个连续的红色结点。此时需要对红黑树分情况来讨论：

在讲解情况三、四、五之前，先说明一下：

• cur为当前节点（关注节点），p(parent)为父节点，g(grandparent)为祖父节点，u(uncle)为叔叔节点；
• cur不一定就是新插入的节点，也有可能是因为 cur 的子树在调整的过程中将 cur 节点的颜色由黑色改成红色。

5.1 情况一：u存在且为红

情况一: cur为红，p为红，g为黑，u存在且为红

抽象分析：

1. 因为cur和p都为红色违反性质3，所以一定要把p变为黑色。
2. 但只变p又违反性质4各路径上黑色节点的数量不同，所以要把u也变为黑色。
3. 但原来所有路径上只有1个黑色节点（可见的）而现在变为2个。如果g树是子树，又会使整棵树违反性质4。所以要把g变为红色。
4. g的父节点也可能是红色，所以要继续向上调整。

解决方式：变色并继续向上调整

1. 将p,u都改为黑色，g改为红色；
2. 如果g不为根，就把g当成cur继续向上调整；
3. 如果g为根，就把g变为黑色。性质2：根节点是黑色的。

具体分析：

cur就是新插入的节点：

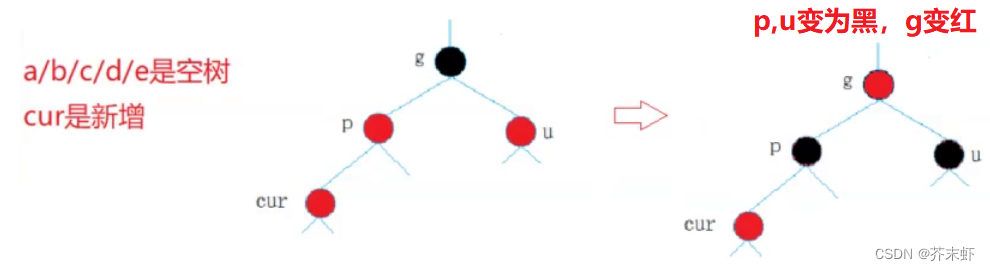
cur节点原来是黑色之后又被调整为红色：

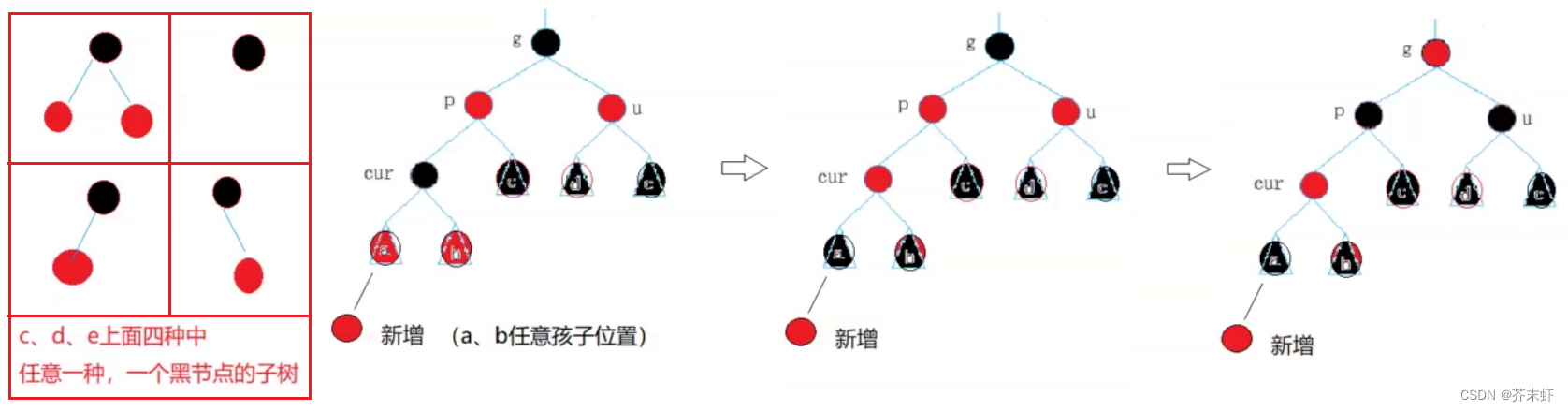
注意：a,b,c,d,e可能是连续的几层黑色节点（要求每条路径的黑色节点数量相同），然后才出现上述情况。因为情况太多，过于复杂故作省略。

---

5.2 情况二：u不存在/u存在且为黑（单旋）

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑（单旋）

抽象分析：

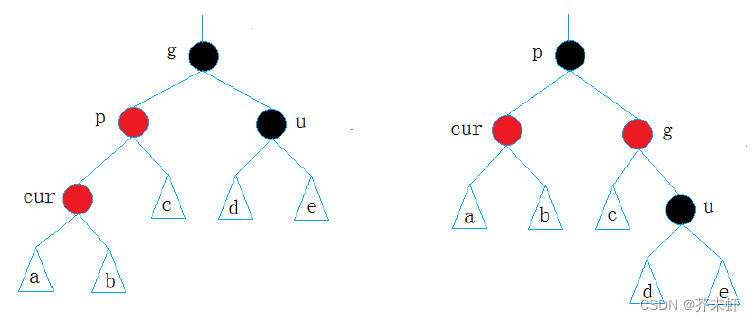
1. 因为cur和p都为红色违反性质3，所以一定要把p变为黑色。
2. 但只变p使左路黑节点+1违反性质4，因此还要以g为轴点右单旋，使左路黑节点-1。
3. 但此时由于右单旋使右路黑节点+1，所以要将g变为红色，右路黑节点-1。最终满足性质4。

解决方式：单旋+变色

1. 如果p为g的左孩子，cur为p的左孩子（左左），则对g进行右单旋；
2. 如果p为g的右孩子，cur为p的右孩子（右右），则对g进行左单旋；
3. p、g变色–p变黑色，g变红色。
4. 完成旋转变色后每条路径的黑节点数量相同且与插入前也相同，并且根节点为黑色不需要继续往上处理。

具体分析：u 的情况有两种

uncle节点不存在：

如果 u 节点不存在，则 cur 一定是新插入节点，因为如果 cur 不是新插入节点，则 cur 和 p 一定有一个节点的颜色是黑色，就不满足性质4：每条路径黑色节点个数相同。

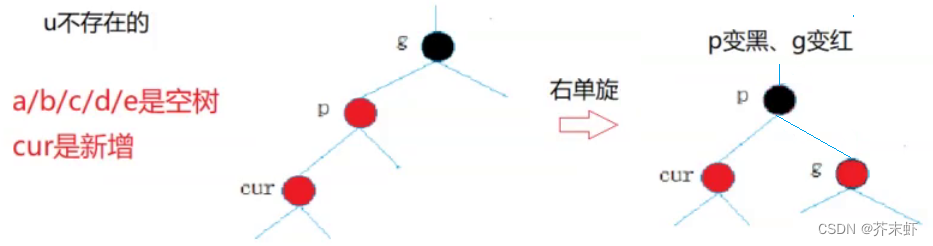
uncle节点存在且为黑色：

如果 u 节点存在且为黑色，那么 cur 节点原来的颜色也一定是黑色的，现在看到其是红色的原因是因为 cur 的子树在调整的过程中将 cur 节点的颜色由黑色改成红色。

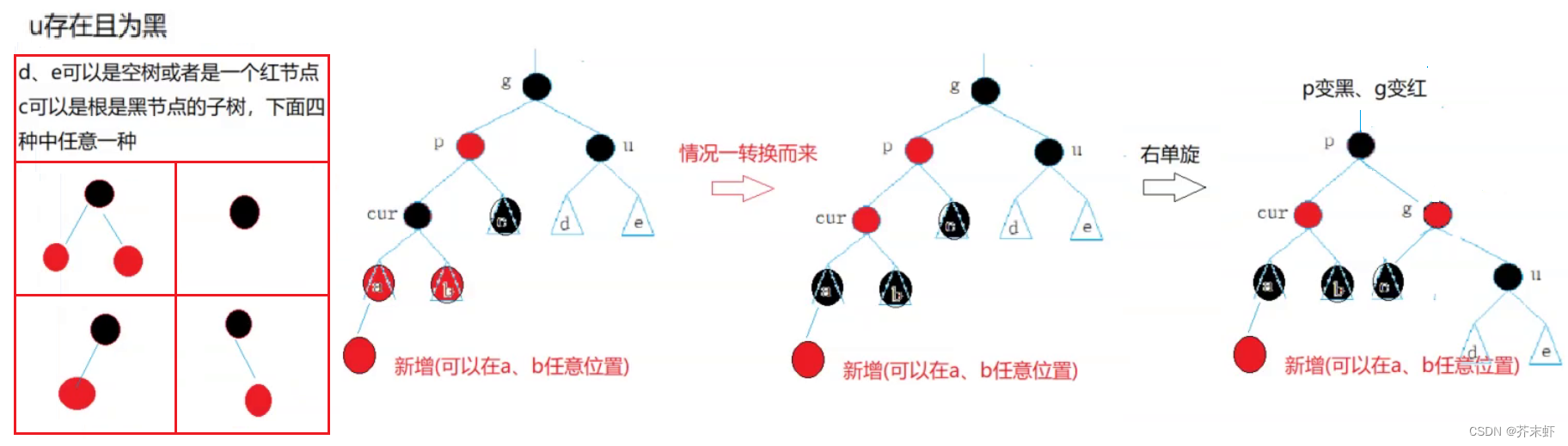
注意：a,b,c,d,e可能是连续的几层黑色节点（要求每条路径的黑色节点数量相同），然后才出现上述情况。因为情况太多，过于复杂故作省略。

---

5.3 情况三：u不存在/u存在且为黑（双旋）

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑（双旋）

抽象图：

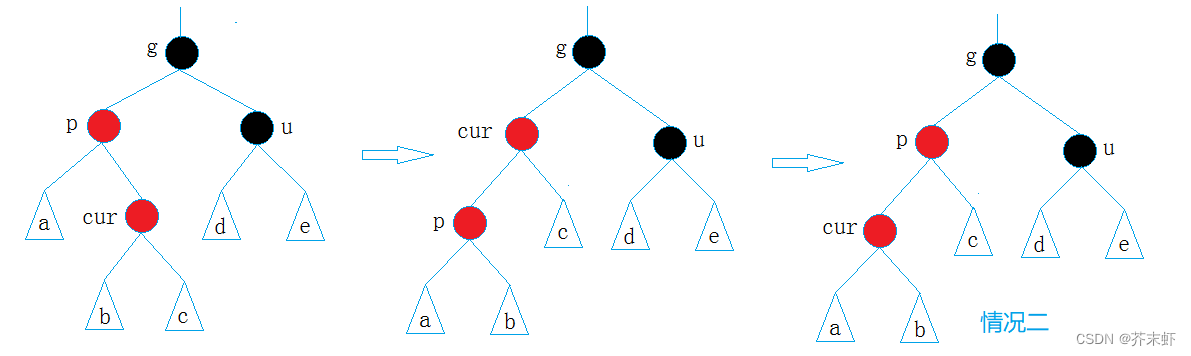
情况三先以p为轴点左单旋，转换为情况二。

解决方式：双旋+变色

1. p为g的左孩子，cur为p的右孩子（左右），则先对p做左单旋，再对g做右单旋；
2. p为g的右孩子，cur为p的左孩子（右左），则先对p做右单旋，再对g做左单旋；
3. cur、g变色–cur变黑色，g变红色。
4. 完成旋转变色后每条路径的黑节点数量相同且与插入前也相同，并且根节点为黑色不需要继续往上处理。

具体分析：

uncle节点不存在

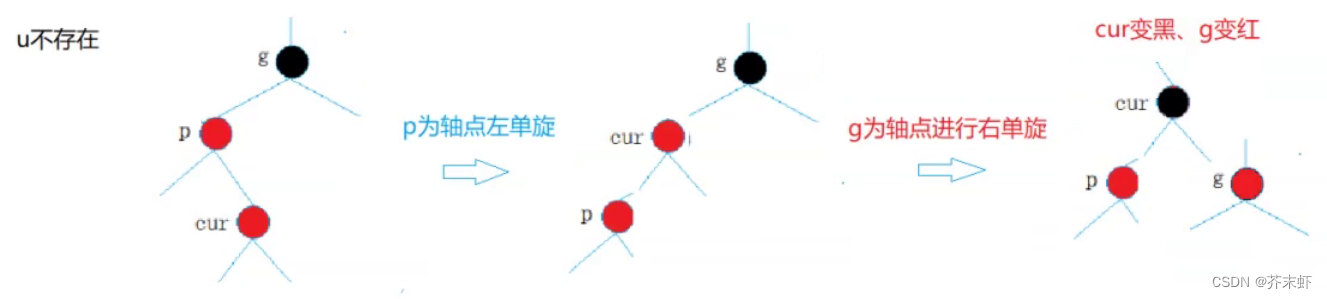
uncle节点存在且为黑色：

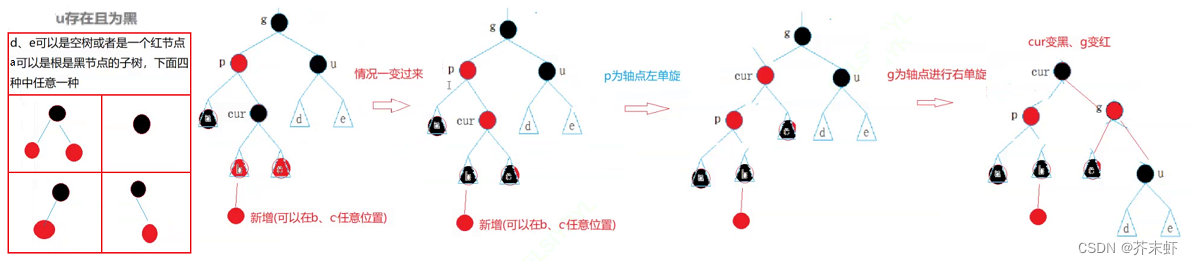
注意：a,b,c,d,e可能是连续的几层黑色节点（要求每条路径的黑色节点数量相同），然后才出现上述情况。因为情况太多，过于复杂故作省略。

总结：

• 二叉树插入操作的难点在于通过变色和旋转操作恢复红黑树的性质，性质得到满足红黑树就能做到近似平衡：最长路径不超过最短路径的两倍。
• 恢复的最终目的：1.关注子树满足红黑树的所有性质 2.插入前后关注子树每条路径的黑节点数量不变（保证整棵树的性质4）

---

5.4 插入代码

bool Insert(const pair<K,V> &kv)
{//1. 按照二叉搜索的树规则插入新节点Node* &root = GetRoot(); //这里注意要用引用接收返回值if(root == nullptr){//如果新插入的节点是根节点，需要将节点变为黑色以满足性质2root = new Node(kv, BLACK); //因为GetRoot返回指针的引用，所以改的实际是_phead->_parentroot->_parent = _phead;_phead->_left = root;_phead->_right = root;return true;}Node *cur = root;Node *parent = nullptr;while(cur != nullptr){if(kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first){parent  = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv,RED); //新插入的节点默认是红色的if(kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//2.检测新节点插入后，红黑树的性质是否造到破坏。//如果父节点是黑色的，没有违反红黑树的任何性质，则不需要调整；//但如果父节点颜色为红色时，就违反了性质3：路径上不能有两个连续的红色结点。//上一次循环中grandparent 为根节点，此次循环parent == _pheadwhile(parent != _phead && parent->_color == RED) {Node *grandparent = parent->_parent;//断言检查：grandparent一定不为空且为黑色！assert(grandparent != nullptr);assert(grandparent->_color == BLACK);Node *uncle = grandparent->_left;if(parent == grandparent->_left)uncle = grandparent->_right;if(uncle != nullptr && uncle->_color == RED) //情况一：uncle存在且为红{parent->_color = uncle->_color = BLACK; //变色grandparent->_color = RED;cur = grandparent; //继续向上调整parent = cur->_parent;}else //情况二、三：uncle不存在或uncle存在且为黑{if(parent == grandparent->_left){if(cur == parent->_left) //左左{RotateR(grandparent); //右单旋parent->_color = BLACK; //变色grandparent->_color = RED;}else{ //左右RotateL(parent); //左右双旋RotateR(grandparent);cur->_color = BLACK; //变色grandparent->_color = RED;}}else{if(cur == parent->_right) //右右{RotateL(grandparent); //左单旋parent->_color = BLACK; //变色grandparent->_color = RED;}else{ //右左RotateR(parent); //右左双旋RotateL(grandparent);cur->_color = BLACK; //变色grandparent->_color = RED;}}//旋转变色后无需继续调整，直接退出循环。break; } //end of else} //end of while//如果在调整过程中将根节点变为红色，记得重新变回黑色。if(parent == _phead) root->_color = BLACK;//令头节点的左指针指向红黑树的最左节点_phead->_left = LeftMost();//令头节点的右指针指向红黑树的最右节点_phead->_right = RightMost();return true;
}

---

5.5 旋转代码

void RotateL(Node *parent){Node *subR = parent->_right;Node *subRL = subR->_left;Node *ppNode = parent->_parent;parent->_right = subRL;if(subRL != nullptr){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if(ppNode == _phead){_phead->_parent = subR;}else{if(ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}}subR->_parent = ppNode;
}void RotateR(Node *parent){Node *subL = parent->_left;Node *subLR = subL->_right;Node *ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;parent->_left = subLR;if(subLR != nullptr)subLR->_parent = parent;if(ppNode == _phead){ppNode->_parent = subL;}else{if(ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}}subL->_parent = ppNode;
}

---

六、查找和遍历

Node* Find(const K &k){Node *root = GetRoot();if(root == nullptr)return nullptr;Node *cur = root;while(cur != nullptr){if(k > cur->_kv.first){cur = cur->_right;}else if(k < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;
}void Inorder(){_Inorder(GetRoot());cout << endl;
}void _Inorder(Node *root){if(root == nullptr) return; _Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_Inorder(root->_right);
}

---

七、红黑树的验证

红黑树的检测分为两步：

1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质

bool IsValidRBTree(){Node *root = GetRoot();//空树也是红黑树if(root == nullptr) return true;//检查性质2:if(root->_color != BLACK){cout << "违反性质2：根节点不为黑色！" << endl;return false;}//检查性质3,4：int benchmark = 0;return _IsValidRBTree(root, 0, benchmark);
}//blacknum：用于记录当前路径的黑色节点个数，不能传引用。
//benchmark：用于记录第一条路径的黑色节点个数。需要传引用，返回给上层递归。
bool _IsValidRBTree(Node *root, int blacknum, int &benchmark){if(root == nullptr){if(benchmark == 0) //表示第一条路径遍历完{benchmark = blacknum; //记录第一条路径的黑色节点个数return true;}else{if(blacknum != benchmark) //如果其他路径的blacknum与第一条路径不同，说明违反性质4{cout << "违反性质4：从任意节点到每个叶子节点的所有路径都包含相同数目的黑色节点！" << endl;return false;}else{return true;}}}//检查性质3：if(root->_color == RED && root->_parent->_color == RED){cout << "违反性质3：路径上有两个连续的红色节点！" << endl;return false;}if(root->_color == BLACK){++blacknum; }return _IsValidRBTree(root->_left, blacknum, benchmark)&& _IsValidRBTree(root->_right, blacknum, benchmark);
}