商丘做网站用什么程序好如何引流客源最快的方法
文章目录
- 前言
- 一、 什么是补零
- 二、案例
- 三、补零前仿真及分析
- 1、补零前 MATLAB 源码
- 2、仿真及结果分析
- 四、补零后仿真及分析
- 1、补6000个零且1000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 2、波形分辨率
- 3、补6000个零且7000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 4、补7000个零且7000采样点
- ①、 MATLAB 源码
- ②、仿真及结果分析
- 五、补零的好处
- 六、资源自取
前言
本文对信号补零前与补零后分别做 FFT,对频谱进行分析。
先抛出结论:
补 1 次零相当于在原始频谱图中每两个频率之间插入1个频率值,补 2 次零相当于在原始频谱图中每两个频率之间插入 2 个频率值,并且原始频率值的位置及其幅值保持不变。因此, 补零会使频谱图中的频率点的数量增加,从而使得频谱图更加的光滑连续,但是补零不能对频谱图中的频率分辨率、频率值以及幅值有所改善。
一、 什么是补零
FFT 运算点数( M M M) > 采样点数( N N N)时, f f t ( x n , M ) fft(xn,M) fft(xn,M) 函数对信号 x n x_n xn 进行尾补零操作即在该信号尾部添加多个值为 0 的数据点以使信号总点数 N N N 增至 FFT 运算所需点数 M M M。
二、案例
目前有一个信号 ,这个信号中仅包含两个正(余)弦波,一个是 1 M H z 1MHz 1MHz,一个是 1.5 M H z 1.5MHz 1.5MHz,即 x = c o s ( 2 π ∗ 1000000 t ) + c o s ( 2 π ∗ 1050000 t ) x=cos(2\pi*1000000t)+cos(2\pi*1050000t) x=cos(2π∗1000000t)+cos(2π∗1050000t)。设定采样频率为 F s = 100 M H z F_s=100MHz Fs=100MHz,如果采 1000 个点,那么时域信号的时长就有 10 μ s 10\mu s 10μs。(采样率*采样时间=采样点数)
三、补零前仿真及分析
直接对这 1000 个数据点做 FFT
1、补零前 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 1000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [未补零 被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [未补零 被采信号 && 绘制频谱图]
M = 1000; % FFT 运算点数
X = fft(xn, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('xn 频谱图');
ylabel('X(f)');
xlabel('频率/Hz');
2、仿真及结果分析
①、 x n x_n xn 时域图
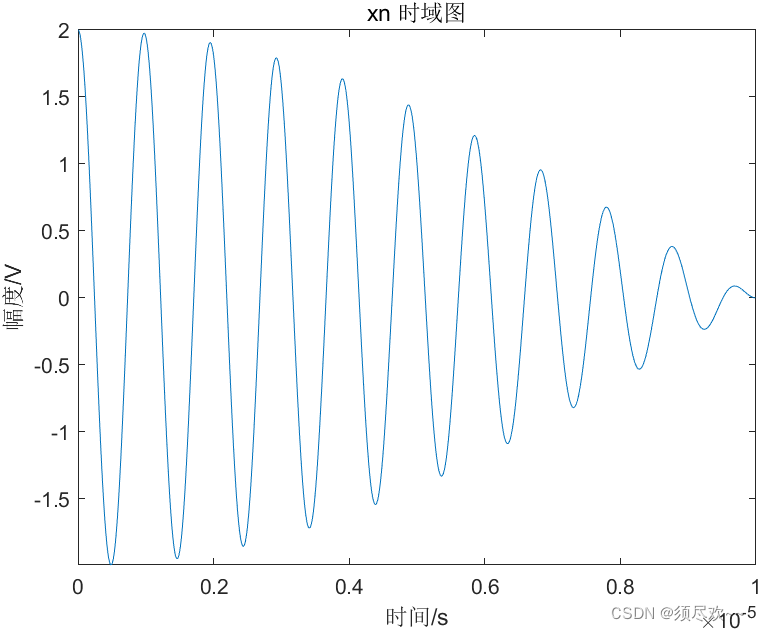
②、 x n x_n xn 频谱图
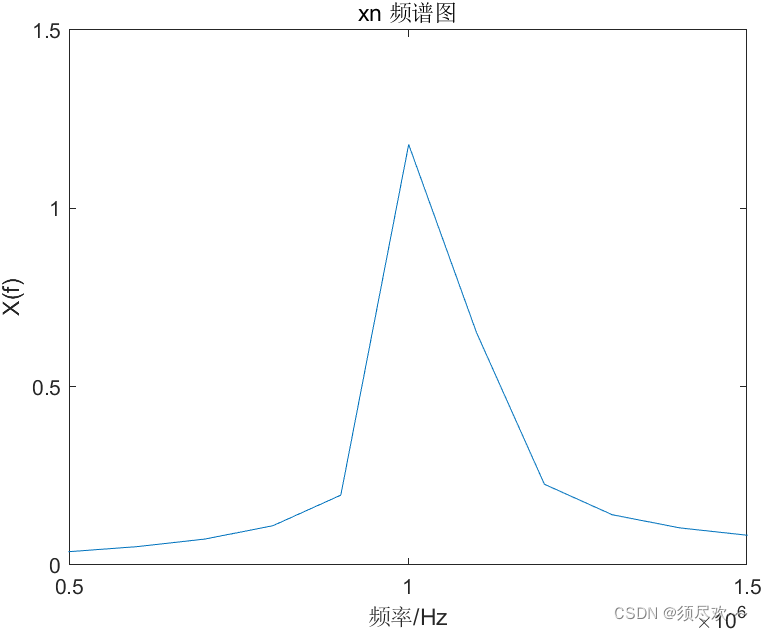
如上图所示,直接对这 1000 个数据点做快速傅里叶变换,将得到频谱,只有一个谱峰,在 1 M H z 1MHz 1MHz 的地方,由于频谱点稀疏,在 1 M H z 1MHz 1MHz 根本无法将 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 的两个频率分开,这是因为频率分辨率不够,采样率 100 M H z 100MHz 100MHz,FFT 点数 1000 个点,频率分辨率 = 采样率 /FFT 点数 = 100 K H z 100 KHz 100KHz,所以无法区分 50 K H z 50KHz 50KHz。
四、补零后仿真及分析
对数据补零,增加 FFT 点数,比如补 6000 个零,做 7000 个点的 FFT。
1、补6000个零且1000采样点
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 1000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,6000)]; % 补6000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('补零后共7000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析
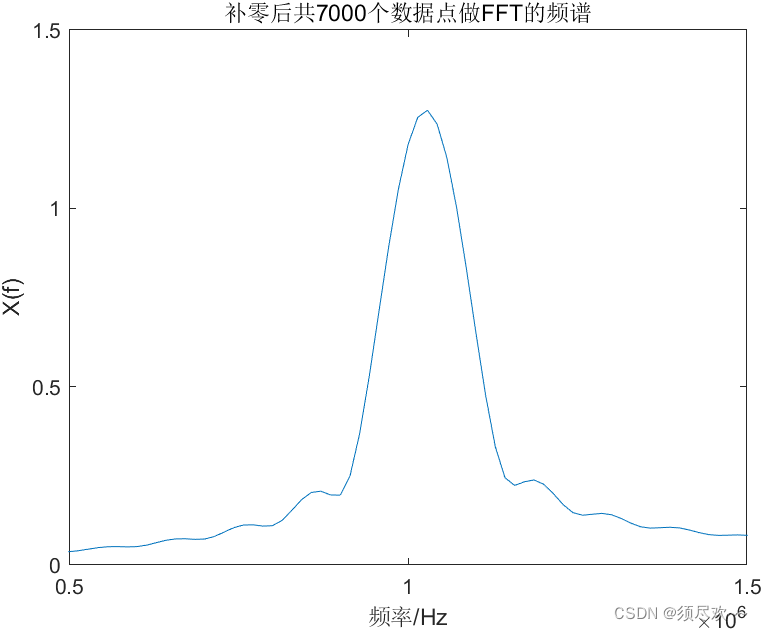
可以看到信号频谱变得平滑了,但是仍然无法区分 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz
这里就要引出一个波形分辨率的概念,虽然补零了,提高了频谱分辨率,但是无法提高波形分辨率
2、波形分辨率
发现频率成分无法被区分开,第一反应就是:频率分辨率不够,那么,如何提高频率分辨率呢?首先要清楚,这里存在两种类型的频率分辨率。
一种叫波形分辨率,其由原始数据的时间长度决定:
Δ R w = 1 T \Delta R_w=\frac{1}{T} ΔRw=T1
另一种可以称之为视觉分辨率或FFT分辨率,其由采样频率和参与 FFT 的数据点数决定:
Δ R f f t = F s N f f t \Delta R_{fft}=\frac{F_s}{N_{fft}} ΔRfft=NfftFs
之所以要区分,就是因为后面要进行 “补零” 操作。如果不补零,直接对原始数据做 FFT,那么这两种分辨率是相等的。
例如上面,有:
Δ R w = 1 10 μ s = Δ R f f t = 100 M H z 1000 = 100 K H z \Delta R_w=\frac{1}{10\mu s}=\Delta R_{fft}=\frac{100MHz}{1000}=100KHz ΔRw=10μs1=ΔRfft=1000100MHz=100KHz
所以要想提高波形分辨率,必须提高信号数据本身的长度
3、补6000个零且7000采样点
采样 7000 个信号数据做 FFT,还是补 6000 个零 ,做 7000 个点的 FFT
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 7000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,6000)]; % 补6000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('采样点7000且补零后共7000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析
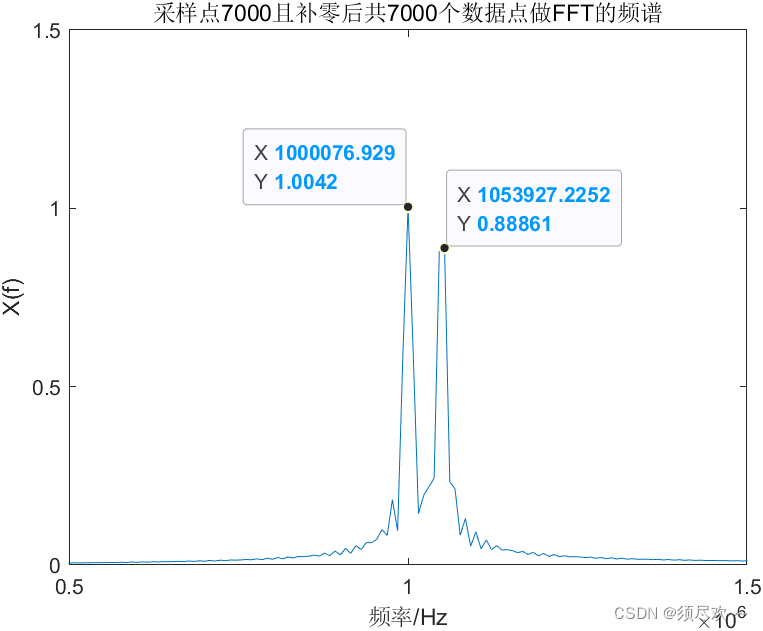
因为此时的波形分辨率为: Δ R w = 1 70 μ s ≈ 14 K H z \Delta R_w=\frac{1}{70 \mu s}\approx14KHz ΔRw=70μs1≈14KHz,小于 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 这两个频率成分之间的举例 50 K H z 50KHz 50KHz,所以可以看出有两个明显的峰值。
但是会发现 1 M H z 1MHz 1MHz 对应的幅值为 1,与原始信号中该频率成分的幅值一致,但是 1.05 M H z 1.05MHz 1.05MHz 对应的幅值明显低于 1,但是其周边的点上确有不小的幅值,这就是所谓的频谱泄露,因为数据点的个数影响,使得在 1 M H z 1MHz 1MHz 处有谱线存在,但在 1.05 M H z 1.05MHz 1.05MHz 处没有谱线存在,使测量结果偏离实际值,同时在实际频率点的能量分散到两侧的其他频率点上,并出现一些幅值较小的假谱。
这是因为在 1.05 M H z 1.05MHz 1.05MHz 那个地方刚好有个频点,也就是出现了所谓的频谱泄漏,还是数据长度不够,但这时是可以通过补零来达到目的。补零 1000 个点,做 8000 点的FFT。
4、补7000个零且7000采样点
采样 7000 个信号数据做 FFT,补 7000 个零 ,做 8000 点的 FFT
①、 MATLAB 源码
%% [预处理]
clc; % 清除命令窗口
clear; % 清除工作空间的变量和函数
clf; % 清除当前图形%% [采样参数]
fs = 100e6; % 采样频率 (Hz)
ts = 1/fs; % 采样周期 (s)
N = 7000; % 采样点数 (个)
n = 0:N-1; % 采样点索引
t = n*ts; % 采样时间轴%% [被采信号 && 绘制时域波形]
fa = 1e6; % 信号 a 的频率
fb = 1.05e6; % 信号 b 的频率
xn = cos(2*pi*fa*t) + cos(2*pi*fb*t); % 被采信号 = 信号a + 信号bfigure(1);
plot(t, xn);
axis([0 10e-6 -inf inf]); % x 轴范围设置成[0,10us],y 轴范围最小值和最大值都为无穷
title('xn 时域图');
ylabel('幅度/V');
xlabel('时间/s');%% [尾补零 被采信号 && 绘制时域波形]
xnwei=[xn zeros(1,7000)]; % 补7000个零
M = length(xnwei); % FFT 运算点数
X = fft(xnwei, M); % FFT 输出值
X = [X(1)/N,X(2:M)*2/N]; % 幅度轴,对FFT输出值进行归一化处理,得到幅度轴上的值。
k = 0:M-1; % 频率点索引
f = fs*k/(M-1); % 频率轴figure(2);
plot(f, abs(X));
axis([0.5e6 1.5e6 0 1.5]); % x 轴范围设置成[0.5e6,1.5e6],y 轴范围设置成[0,1.5]
title('采样点7000且补零后共8000个数据点做FFT的频谱');
ylabel('X(f)');
xlabel('频率/Hz');
②、仿真及结果分析

FFT 分辨率为 F s / N = 100 M H z / 8000 = 12.5 K H z F_s/ N=100MHz/8000=12.5KHz Fs/N=100MHz/8000=12.5KHz,是这两个频率的公约数, 1 M H z = 80 ∗ 12.5 K H z 1MHz = 80*12.5KHz 1MHz=80∗12.5KHz, 1.05 M H z = 84 ∗ 12.5 K H z 1.05MHz=84*12.5KHz 1.05MHz=84∗12.5KHz,所以谱线同时经过 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 这两个点。
从上图也可以看到效果也比较理想,将 1 M H z 1MHz 1MHz 和 1.05 M H z 1.05MHz 1.05MHz 的两个信号频率分开。
五、补零的好处
- 使数据 N 为 2 的整次幂,便于使用 FFT
- 补零后,其实是对 DFT 结果做了插值,克服“栅栏"效应,使谱外观平滑化。我把“栅栏"效应形象理解为,就像站在栅栏旁边透过栅栏看外面风景,栅栏会挡住比较多风景,此时就可能漏掉较大频域分量,但是补零以后,相当于你站远了,风景就看的越来越清楚了。
- 由于对时域数据的截短必然造成频谱泄露,因此在频谱中可能出现难以辨认的谱峰,补零在一定程度上能消除这种现象。
对信号进行头补零或尾补零再得到的幅频响应相等,相频响应不同
补零会使频谱图中的频率点的数量增加,从而使得频谱图更加的光滑连续,但是补零不能对频谱图中的频率分辨率、频率值以及幅值有所改善。
- 补零(Zero-padding)是在FFT计算中向输入信号序列的末尾添加零值,从而增加信号的长度。这样做的主要目的是在频域中插入更多的零频率样本,以获得更好的频谱分析图。
- 补零可以在一定程度上改善频谱图的可视化效果,使频谱图在频率轴上呈现更平滑的外观。这是因为补零增加了离散傅里叶变换(DFT)点数,从而在频率轴上产生更多的插值点。然而,这并不意味着补零改善了频率分辨率或精确性。
- 频率分辨率由采样率和FFT长度决定,而补零并不改变采样率。补零只是对现有的采样点进行插值,不会增加频率分辨率。实际上,补零只是在现有的频率分辨率上插入了更多的点,而不是提高了分辨率本身。
- 频率值和幅值也不会因为补零而改变。补零只是在现有的频率轴上插入了更多的点,对原有的频率值和幅值进行了插值。这些插值点的值是通过对原始采样点进行插值计算得到的,而不是通过补零本身引入的信息。
- 如果希望改善频率分辨率或精确性,需要增加采样率或使用更长的FFT长度。
六、资源自取
信号补零对信号频谱的影响
我的qq:2442391036,欢迎交流!
