电商平台网站大全品牌关键词排名优化怎么做
文章目录
- 竞赛链接
- Q1:8015. 距离原点最远的点(贪心)
- Q2:8022. 找出美丽数组的最小和(贪心)
- Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)
- 思路
- 竞赛时丑陋代码(有一说一没眼看,现在已经忘了当时是怎么想的了)
- 优雅代码
- Q4:2836. 在传球游戏中最大化函数值(⭐⭐⭐⭐⭐树上倍增)
- 解法——利用倍增算法
- 模板题——1483. 树节点的第 K 个祖先
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-360
Q1:8015. 距离原点最远的点(贪心)
https://leetcode.cn/problems/furthest-point-from-origin/
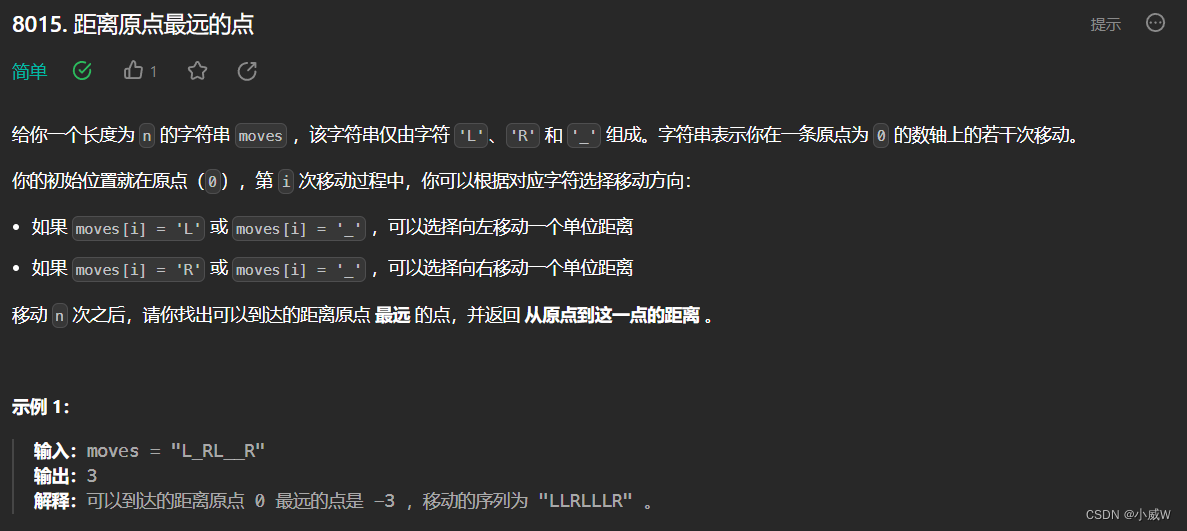
提示:
1 <= moves.length == n <= 50
moves 仅由字符 'L'、'R' 和 '_' 组成
抓住本质,R 和 L 是不能改变的,而 _ 是可以随意选择的,因此可以在最后决定 _ 往哪个方向走。
class Solution {public int furthestDistanceFromOrigin(String moves) {int ans = 0, cnt = 0, pos = 0;for (char ch: moves.toCharArray()) {if (ch == 'R') pos++;else if (ch == 'L') pos--;else cnt++;}return Math.abs(pos) + cnt;}
}
Q2:8022. 找出美丽数组的最小和(贪心)
https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
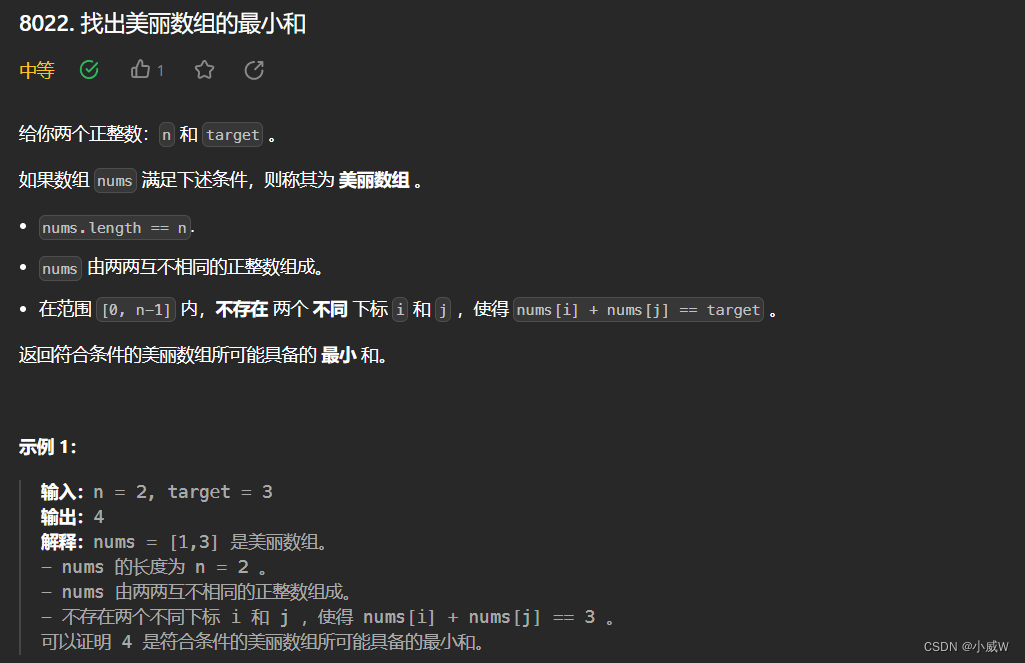
提示:
1 <= n <= 10^5
1 <= target <= 10^5
这道题目和 第 359 场周赛 中的 6450. k-avoiding 数组的最小总和 几乎一样。
我们还是用贪心来解决,从小到大,能选就选。
class Solution {public long minimumPossibleSum(int n, int target) {long ans = 0;Set<Integer> s = new HashSet<>();for (int i = 1; s.size() < n; ++i) {if (!s.contains(target - i)) {s.add(i);ans += i;}}return ans;}
}
Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/
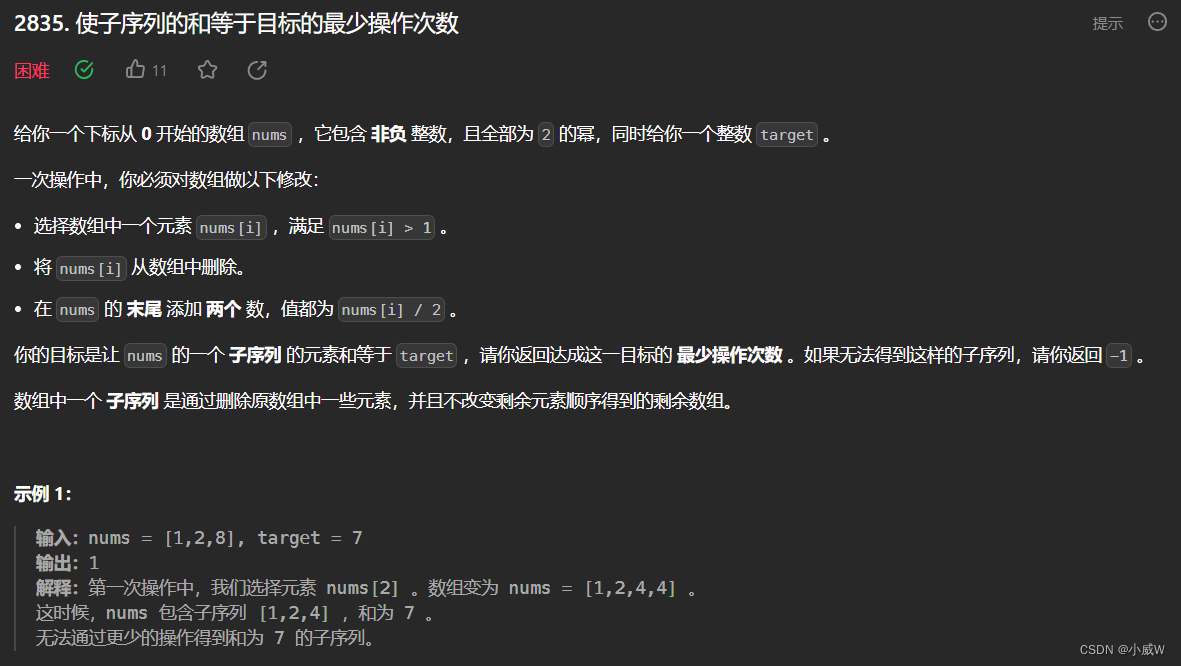
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 2^30
nums 只包含非负整数,且均为 2 的幂。
1 <= target < 2^31
思路
首先确定 sum >= target 则一定有解,否则一定无解。

竞赛时丑陋代码(有一说一没眼看,现在已经忘了当时是怎么想的了)
class Solution {static Map<Integer, Integer> m = new HashMap(), m2 = new HashMap();static {for (int i = 0, v = 1; i <= 30; ++i, v *= 2) {m.put(v, i);m2.put(i, v);}}public int minOperations(List<Integer> nums, int target) {long sum = 0;int[] cnt = new int[31], cnt2 = new int[31];for (int num: nums) {sum += num;cnt[m.get(num)]++;}if (sum < target) return -1;for (int i = 30; i >= 0; --i) {if (target >= m2.get(i)) {cnt2[i]++;target -= m2.get(i);}}int v = 0, ans = 0, last = -1;for (int i = 0; i <= 30; ++i) {if (cnt[i] > cnt2[i]) {if (last != -1) {ans += i - last;last = -1;v += (cnt[i] - cnt2[i] - 1) * m2.get(i);} else {v += (cnt[i] - cnt2[i]) * m2.get(i);}} else if (cnt[i] < cnt2[i]) {if (v >= (cnt2[i] - cnt[i]) * m2.get(i)) {v -= (cnt2[i] - cnt[i]) * m2.get(i);}else if (last == -1) last = i;}}return ans;}
}
优雅代码
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/solutions/2413344/tan-xin-by-endlesscheng-immn/
class Solution {public int minOperations(List<Integer> nums, int target) {long s = 0; // 求和long[] cnt = new long[31]; // 统计2^i的数量for (int x: nums) {s += x;cnt[Integer.numberOfTrailingZeros(x)]++;}if (s < target) return -1; // 无解的情况int ans = 0, i = 0;s = 0;// 注意这里是1L,因为i 最大是 30,这是可以进循环的,但是加一后就变成 31 了,虽然一定不会进入循环,但是要在 while 那里判断一下。while ((1L << i) <= target) {s += cnt[i] << i;int mask = (int) ((1L << ++i) - 1);if (s >= (target & mask)) continue; // 检查当前和能否填补target部分ans++; // 否则需要分解更大的数字while (cnt[i] == 0) {ans++;i++;}}return ans;}
}
Q4:2836. 在传球游戏中最大化函数值(⭐⭐⭐⭐⭐树上倍增)
https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/
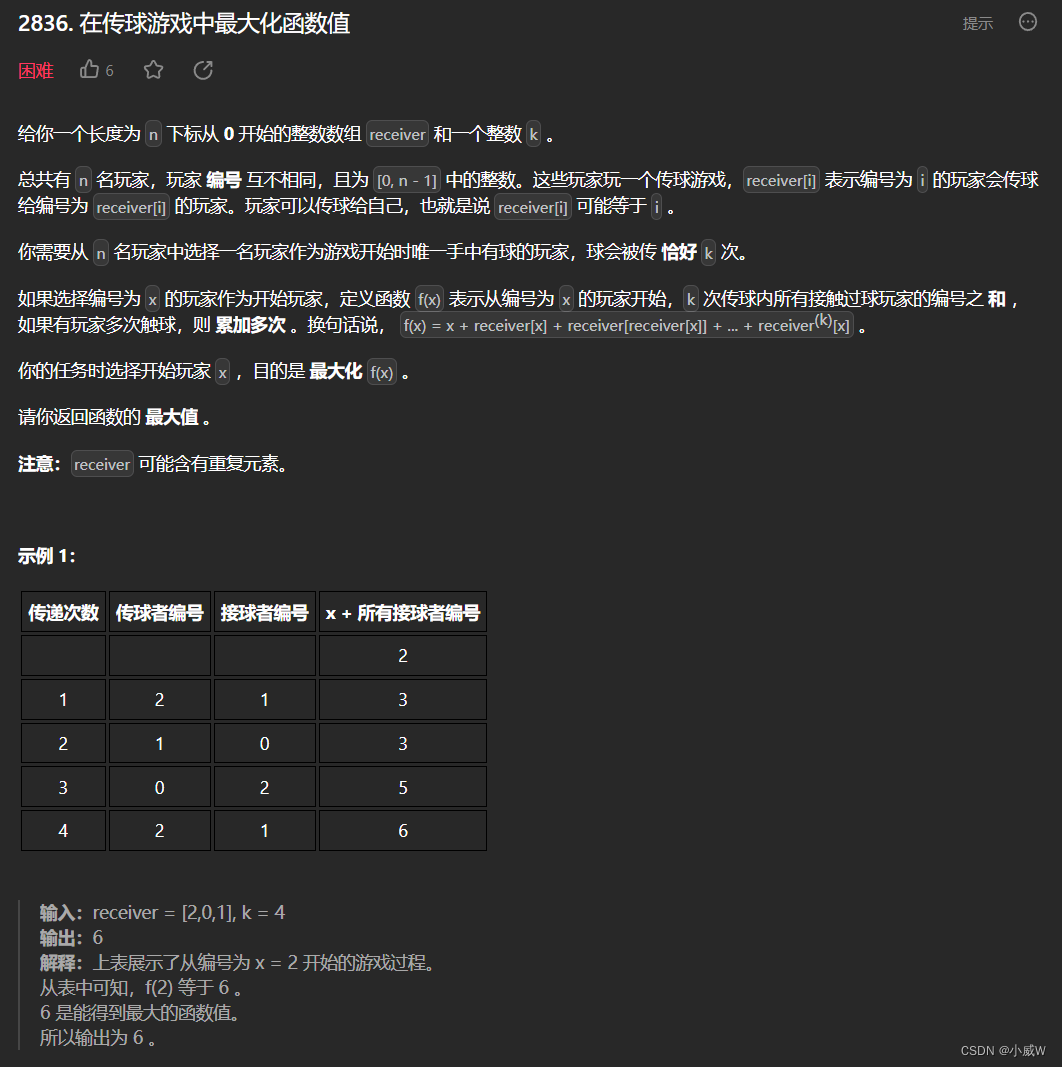
提示:
1 <= receiver.length == n <= 10^5
0 <= receiver[i] <= n - 1
1 <= k <= 10^10
解法——利用倍增算法
利用倍增算法,预处理每个节点 x 的第 2^i个祖先节点,以及从 x 的父节点到 x 的第 2^i 个祖先节点的节点编号之和。最后枚举起点 x,一边向上跳一边累加节点编号。
可以从代码模板中修改过来,多了要维护节点之间的和。
class Solution {public long getMaxFunctionValue(List<Integer> receiver, long k) {int n = receiver.size(); // 节点的个数int m = 64 - Long.numberOfLeadingZeros(k); // k的二进制长度int[][] pa = new int[n][m]; // 节点x的第2^i个祖宗节点的变好long[][] sum = new long[n][m]; // 节点x的父节点到x的第2^i个祖宗节点的节点编号之和// 初始化dp数组for (int i = 0; i < n; ++i) {pa[i][0] = receiver.get(i);sum[i][0] = receiver.get(i);}// 递推dp数组(先枚举i,再枚举x)for (int i = 0; i < m - 1; ++i) { // 注意这里的条件是 i < m - 1for (int x = 0; x < n; ++x) {int p = pa[x][i];pa[x][i + 1] = p < 0? -1: pa[p][i];// 合并节点的和 sum[x][i + 1] = sum[x][i] + sum[p][i]; }}long ans = 0;// 枚举各个节点作为起始节点for (int i = 0; i < n; ++i) {long s = i;int x = i;for (long t = k; t > 0; t &= t - 1) {int ctz = Long.numberOfTrailingZeros(t);// 要先处理求和,再处理节点的变化s += sum[x][ctz]; x = pa[x][ctz];}ans = Math.max(ans, s);}return ans;}
}
受 cpu 缓存的影响,倍增的二维数组开成 log*n 会比 n*log 快很多。
二维数组开成 logn * n 的形状会比开成 n * logn 的形状快很多,是因为在计算机中,连续的内存访问比随机的内存访问更快。当我们按行访问一个二维数组时,我们可以利用缓存行的概念,即将一行的数据读入缓存中,这样下一次访问时就可以直接从缓存中读取数据,而不需要再次从内存中读取。如果我们按列访问二维数组,则每次访问都需要跨越多个缓存行,这样会导致缓存失效,从而降低程序的性能。因此,将二维数组按行存储可以提高程序的性能。
所以可以将代码修改成如下:
class Solution {public long getMaxFunctionValue(List<Integer> receiver, long k) {int n = receiver.size(); // 节点的个数int m = 64 - Long.numberOfLeadingZeros(k); // k的二进制长度int[][] pa = new int[m][n]; // 节点x的第2^i个祖宗节点的变好long[][] sum = new long[m][n]; // 节点x的父节点到x的第2^i个祖宗节点的节点编号之和// 初始化dp数组for (int i = 0; i < n; ++i) {pa[0][i] = receiver.get(i);sum[0][i] = receiver.get(i);}// 递推dp数组(先枚举i,再枚举x)for (int i = 0; i < m - 1; ++i) { // 注意这里的条件是 i < m - 1for (int x = 0; x < n; ++x) {int p = pa[i][x];pa[i + 1][x] = p < 0? -1: pa[i][p];// 合并节点的和 sum[i + 1][x] = sum[i][x] + sum[i][p]; }}long ans = 0;// 枚举各个节点作为起始节点for (int i = 0; i < n; ++i) {long s = i;int x = i;for (long t = k; t > 0; t &= t - 1) {int ctz = Long.numberOfTrailingZeros(t);// 要先处理求和,再处理节点的变化s += sum[ctz][x]; x = pa[ctz][x];}ans = Math.max(ans, s);}return ans;}
}
执行用时从 237ms 加速到了 65ms 。
模板题——1483. 树节点的第 K 个祖先
https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/description/

提示:
1 <= k <= n <= 5 * 10^4
parent[0] == -1 表示编号为 0 的节点是根节点。
对于所有的 0 < i < n ,0 <= parent[i] < n 总成立
0 <= node < n
至多查询 5 * 10^4 次
https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/solutions/2305895/mo-ban-jiang-jie-shu-shang-bei-zeng-suan-v3rw/

本质上是动态规划,记 pa[x][i] 为每个节点 x 的第 2^i 个祖先节点。(如果不存在则为 -1)。
计算方式如下:

pa[x][1] = pa[pa[x][0]][0] 的意思是,x 节点的爷爷是 x 节点的父亲的父亲。
一般的,有 pa[x][i + 1] = pa[pa[x][i]][i]。
class TreeAncestor {int[][] pa;// 使用原始数据将整个 pa 数组预处理出来public TreeAncestor(int n, int[] parent) {int m = 32 - Integer.numberOfLeadingZeros(n); // n的二进制长度pa = new int[n][m]; // 表示节点i的2^j个祖宗节点// 初始化dp数组,即填充每个节点的父亲节点for (int i = 0; i < n; ++i) {pa[i][0] = parent[i];}// 先枚举i,再枚举x// 相当于先算出所有爷爷节点,再算出所有爷爷的爷爷节点for (int i = 0; i < m - 1; i++) {for (int x = 0; x < n; ++x) {int p = pa[x][i]; // 取出x的第2^i个祖宗节点// x的第2^(i+1)个祖宗节点 等于 x的第2^i个祖宗节点的第2^i个祖宗节点pa[x][i + 1] = p < 0? -1: pa[p][i]; }}}// 取出node节点的第k个祖宗节点public int getKthAncestor(int node, int k) {// 写法1 从低位到高位枚举// int m = 32 - Integer.numberOfLeadingZeros(k); // k的二进制长度// for (int i = 0; i < m; ++i) {// if ((k >> i & 1) == 1) { // k的二进制当前位为1// node = pa[node][i];// if (node < 0) break;// }// }// return node;// 写法2 不断去掉k末尾的1for (; k != 0 && node != -1; k &= k - 1) {node = pa[node][Integer.numberOfTrailingZeros(k)];}return node;}
}/*** Your TreeAncestor object will be instantiated and called as such:* TreeAncestor obj = new TreeAncestor(n, parent);* int param_1 = obj.getKthAncestor(node,k);*/
成绩记录

最后一题实在是写不出来了。(不过还好好像大家也都写不出来)