自己做网站靠什么赚钱吗谷歌浏览器下载手机版
文章目录
- 1. 投影平面
- 2. Arnoldi Iteration
- 3. python 代码
1. 投影平面
假设我们有一个向量q,我们需要关于向量q,构建一个投影平面P,使得给定任何向量v,可以通过公式 p = P v p=Pv p=Pv,快速得到向量v在投影平面P上的投影向量p.
- 计算向量内积,向量v在向量q上的投影长度|p|
v T q = ∣ v ∣ ∣ q ∣ cos θ = ∣ p ∣ ∣ q ∣ → ∣ p ∣ = v T q ∣ q ∣ \begin{equation} v^Tq=|v||q|\cos{\theta}=|p||q|\rightarrow |p|=\frac{v^Tq}{|q|} \end{equation} vTq=∣v∣∣q∣cosθ=∣p∣∣q∣→∣p∣=∣q∣vTq - 我们知道,q方向上的单位向量为 q ∣ q ∣ \frac{q}{|q|} ∣q∣q,那么投影向量p可得, v T q v^Tq vTq为标量,
随便放位置
p = ∣ p ∣ ⋅ q ∣ q ∣ = v T q ∣ q ∣ ⋅ q ∣ q ∣ = v T q q T q q \begin{equation} p=|p|\cdot \frac{q}{|q|} =\frac{v^Tq}{|q|}\cdot \frac{q}{|q|}=\frac{v^Tq}{q^Tq}q \end{equation} p=∣p∣⋅∣q∣q=∣q∣vTq⋅∣q∣q=qTqvTqq - 重点!内积可以随便转换,并且标量位置可以随便放!
v T q = q T v \begin{equation} v^Tq=q^Tv \end{equation} vTq=qTv - 整理可得:
p = q T v q T q q = q T v q q T q \begin{equation} p=\frac{q^Tv}{q^Tq}q=\frac{q^Tvq}{q^Tq} \end{equation} p=qTqqTvq=qTqqTvq - 标量位置随意可得: q T v q → q q T v q^Tvq\rightarrow qq^Tv qTvq→qqTv
p = q T v q q T q = q q T q T q v \begin{equation} p=\frac{q^Tvq}{q^Tq}= \frac{qq^T}{q^Tq}v \end{equation} p=qTqqTvq=qTqqqTv - 第一个是投影矩阵P
P = q q T q T q , p = P v \begin{equation} P=\frac{qq^T}{q^Tq},p=Pv \end{equation} P=qTqqqT,p=Pv - 第二,快速计算一个向量v在向量q上的投影p
p = q T v q q T q \begin{equation} p=\frac{q^Tvq}{q^Tq} \end{equation} p=qTqqTvq - 第三,当q为单位向量的时候, q T q = ∣ q ∣ 2 = 1 q^Tq=|q|^2=1 qTq=∣q∣2=1,像不像二次型形式,就是这么神奇!
p = q T v q \begin{equation} p=q^Tvq \end{equation} p=qTvq - 第四 ,一般情况下计算垂直向量e,向量几何关系可得v=p+e,
e = v − p = v − q T v q q T q \begin{equation} e=v-p=v-\frac{q^Tvq}{q^Tq} \end{equation} e=v−p=v−qTqqTvq
第五,特殊情况下,|q|=1,整理可得:
e = v − q T v q \begin{equation} e=v-q^Tvq \end{equation} e=v−qTvq

2. Arnoldi Iteration
arnoldi Iteration的作用是想在原来的krylov 子空间中增加一个向量 A q k Aq_k Aqk,具体思路如下图所示:


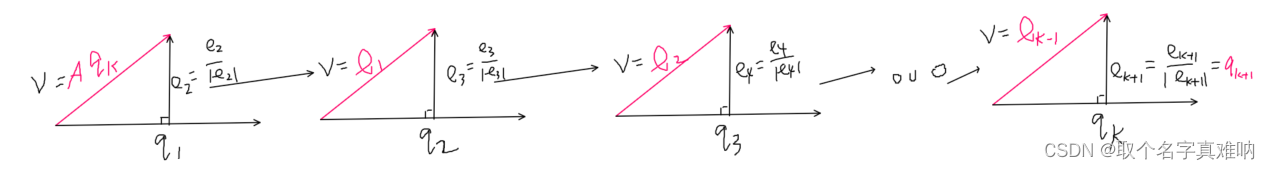
- 小结:arnoldi Iteration 本质上就是新建一个向量 v v v,为了让v向量和以前已知的向量 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk垂直,通过不断迭代,将v向量减去掉所有在 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk上的投影向量 e k e_k ek,这样最后得到的向量 q k q_k qk就一定是垂直于 q 1 , q 2 , ⋯ , q k q_1,q_2,\cdots,q_k q1,q2,⋯,qk
3. python 代码
后续提供详细的,现在直接粘贴吧。
import numpy as npdef arnoldi_iteration(A, b, k):"""Perform Arnoldi iteration to generate an orthonormal basis for the Krylov subspace.Parameters:A : numpy.ndarrayThe input matrix (n x n).b : numpy.ndarrayThe initial vector (n, ).k : intThe number of iterations, which defines the size of the Krylov subspace.Returns:Q : numpy.ndarrayThe orthonormal basis for the Krylov subspace (n x (k+1)).H : numpy.ndarrayThe Hessenberg matrix (k+1 x k)."""n = A.shape[0]Q = np.zeros((n, k + 1)) # Orthonormal basisH = np.zeros((k + 1, k)) # Hessenberg matrix# Normalize the initial vectorQ[:, 0] = b / np.linalg.norm(b)for j in range(k):v = A @ Q[:, j] # Matrix-vector multiplicationfor i in range(j + 1):H[i, j] = np.dot(Q[:, i].conj(), v) # Project v onto the current basis vectorsv = v - H[i, j] * Q[:, i] # Make v orthogonal to Q[:, i]H[j + 1, j] = np.linalg.norm(v) # Normalize v to get the next basis vectorif H[j + 1, j] != 0 and j + 1 < k:Q[:, j + 1] = v / H[j + 1, j]return Q, H# Example usage
if __name__ == "__main__":# Define a random matrix A and a random vector bA = np.random.rand(5, 5)b = np.random.rand(5)k = 4Q, H = arnoldi_iteration(A, b, k)print("Orthonormal basis Q:\n", Q)print("Hessenberg matrix H:\n", H)