当前位置：首页 > news >正文

泗洪网站在线工具网站

news 2025/8/2 16:35:53

泗洪网站,在线工具网站,响应式页面,网站开发文档管理工具第5章状态空间模型和卡尔曼滤波状态空间模型通常试图描述具有两个特征的现象有一个底层系统具有时变的动态关系，因此系统在时间上的“状态”t 与系统在时间的状态t−1有关 .如果我们知道系统在时间上的状态t−1 ，那么我们就有了我们需要知道的一切&am…

第5章状态空间模型和卡尔曼滤波

状态空间模型通常试图描述具有两个特征的现象

有一个底层系统具有时变的动态关系，因此系统在时间上的“状态”t 与系统在时间的状态t−1有关 .如果我们知道系统在时间上的状态t−1 ，那么我们就有了我们需要知道的一切，以便对当时的状态进行推断或预测t .
我们无法观察到系统的真实底层状态，而是观察它的嘈杂版本。

这两个特征导致我们指定状态方程，它描述了系统如何从一个时间点演变到下一个时间点，以及观察方程，它描述了底层状态如何转换（添加噪声）为我们直接测量的东西。

假设有一个初始状态 $x_0 \sim N(x_0^0,P_0^0)$ .为t=1,2,... 我们希望能够估计后续状态 $x_1,x_2,...$ 在每个时间点，我们都会观察到一些数据 $y_t$ 我们希望将这些数据纳入我们的估计中 $x_t$ .

在最简单的情况下，我们可以提出一个观察方程

$y_t=Ax_t+v_t$

这里 $v_t\sim N(0,\sigma ^2)$ 和状态方程

$x_t =\theta x_{t-1}+w_t$

这里 $w_t\sim N(0,\tau ^2)$ .参数θ τ 和σ 假设是已知的（您可以将它们视为调整参数），并且我们希望生成一个估计值 $x_t$ 对于所有人t 感兴趣。回想一下，我们唯一观察到的是序列 $y_1,y_2,...$

状态空间模型可能最有意义的设置是动态设置，在该设置中，我们尝试估计状态值 $x_t$ 在“实时”中，不知道未来会发生什么。例如，在航天器的制导和导航应用中，我们想知道航天器在太空中行驶时的位置和速度，同时考虑到牛顿运动定律。根据我们对航天器位置和速度的估计，我们需要决定下一步该做什么。这种情况要求我们整合所有可用的信息，以产生最佳的估计。

5.1 示例：一个简单的航天器

假设我们乘坐宇宙飞船前往月球，我们刚刚点燃完引擎，让我们继续前进。当我们在太空中“航行”时，我们想知道我们离地球有多远，我们会定期看到恒星以估计我们的位置。

我们的“状态” $x_t$ 是我们的航天器与地球的径向距离。除非有任何加速度，如果航天器在时间 $t-1$ 的位置是 $p_{t-1}$ ，其速度是 $v_{t-1}$ ，那么牛顿定律告诉我们它在时间 t 的位置是

$p_t = p_{t-1} + v_{t-1}\Delta t + w_t$

$\Delta t$ 是时间点之间经过的时间间隙， $w_t$ 表示一些噪声或轻微扰动（例如 $w_t \sim\mathcal{N}(0,\tau^2)$ 。在某些情况下，我们可能会假设 $w_t=0$ 。因此，这里的状态方程体现了“运动中的物体保持运动”的想法。

我们可以写这个方程，稍微不同，使用向量和矩阵作为

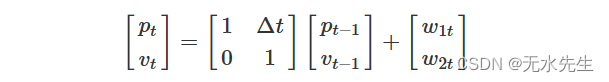
如果实际上没有加速度，我们知道速度不会随时间\（t-1\）到时间\（t\）而变化（也许除了一些轻微的扰动）。如果我们让

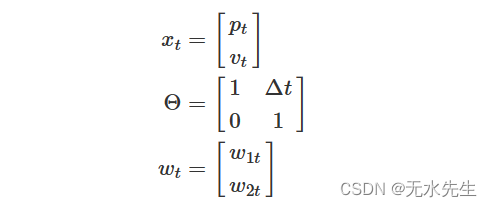
那么我们的状态方程就是

在这一点上，我们还没有讨论数据，但是如果没有对系统的任何观察，我们将不得不假设系统根据状态方程演变。因此，如果我们知道初始状态 $x_0$ ，我们对后续状态的最佳猜测将是

等等。这些与其说是“估计”（因为没有数据），不如说是基于我们对系统潜在动态的了解，对下一个状态应该是什么的预测。

那么问题是，如果我们在时间\ $t$ 观察数据 $y_t$ ，我们应该怎么做？我们期望在时间 t 观察到什么？第二个问题可能是我们需要多久进行一次测量才能很好地估计我们的状态？

现在假设我们偶尔通过在航天器上进行的测量来观察我们的位置，并且在时间 $t$ 我们观察到我们的位置 $y_t$ ，即

$y_t = p_t + v_t$

所以 $y_t$ 是我们真实位置的噪声测量（i.e $v_t \sim\mathcal{N}(0,\sigma^2)$ ）。我们同样可以使用我们的状态向量将其完整形式编写为

$y_ t = [ 1 \; \; \; 0 ] x_ t + v _t$

如果我们让

$A= [\begin{array}{cc} 1 & 0 \end{array}]$

然后我们有 $y_t = Ax_t + v_t$ ，我们的观察方程。一旦我们观察 $y_t$ \ ，我们对 $x_t$ 的知识会如何变化？答案由卡尔曼滤波器给出。

5.2 卡尔曼滤波

有趣的事实：卡尔曼滤波器是由鲁道夫·卡尔曼在马里兰州巴尔的摩高等研究所工作时开发的。

为了介绍卡尔曼滤波器，让我们采用一个简单的模型，有时称为“局部水平”模型，其状态方程为

$x_t=\theta x_{ t-1}+w_t$

和观察方程

$y_t=x_t+v_t$

其中我们假设 $w_t\sim\mathcal{N}(0,\tau^2)$ 和 $v_t\sim\mathcal{N}(0,\sigma^2)$ 。基本的一维卡尔曼滤波算法如下。我们从初始状态 $x_0^0$ 和初始方差 $P_0^0$ 开始。从这里我们计算

$x_1^0 = \theta x_0^0\\P_1^0 = \theta^2 P_0^0 + \tau^2$

作为我们对 $x_1$ 和 $P_1$ 的最佳猜测，给定我们当前状态。鉴于我们的新观察结果 $y_1$ ，我们可以根据这个新信息更新我们的猜测，得到

$x^1_1=x_1^0+K_1(y_1-x^0_1)\\P^1_1=(1-K_1)P^0_1$

这里： $K_1=P^0_1/(P^0_1+\sigma ^2)$

对于一般情况，我们希望生成一个新的估计值 $x_t$ ，并且我们有当前状态 $x_{t-1}^{t-1}$ 和方差 $P_{t-1}^{t-1}$ 。

$x^t_{t-1}=\theta x^{t-1}_{t-1}\\P^t_{t-1}=\theta ^2P^{t-1}_{t-1}+\tau ^2$

鉴于新的信息 $y_t$ ，然后我们可以更新我们的估计以获

$x_t^t=x_t^{t-1}+K_t(y_t-x^{t-1}_t )\\P^t_t=(1-K_t)P^{t-1}_t$

这里：

$K_t = \frac{ P^{t-1}_t}{P^{t-1}_t+\sigma^2 }$

是卡尔曼增益系数。如果我们看一下卡尔曼增益的公式，很明显，如果测量噪声很高，那么 σ 2 很大，那么卡尔曼增益会更接近 0 ，以及新数据点的影响 y t 会很小。如果 σ 2 很小，那么过滤后的值 $X_t^ t$ 将会朝着以下方向进行更多调整 $y_t$ 。在针对特定应用调整卡尔曼滤波算法时，记住这一点很重要。总体思路是

5.3 推导一维情况

有多种方法可以驱动卡尔曼滤波方程，但对于统计学家来说，最简单的方法可能是用正态分布来考虑一切。请记住，我们通常不会相信数据是按正态分布的，但我们可以将正态分布视为一种工作模型。我们将继续使用上面描述的局部模型

$x_t = \theta x_{t-1} + w_t\\ y_t = x_t + v_t$

这里： $w_t\sim\mathcal{N}(0, \tau^2)$ 和 $v_t\sim\mathcal{N}(0,\sigma^2)$

让我们从 t = 1 我们将观察的地方 $y_1$ 。假设我们有初始状态 $X_0 \sim N(X_0^0,P_0^0 )$ 。首先，我们想要得到边际分布 $X_1$ ， IE。 $p (X 1 )$ 。因为没有 $y_0$ 我们还不能以任何观察到的信息为条件。我们可以计算 $p (X 1)$ 作为

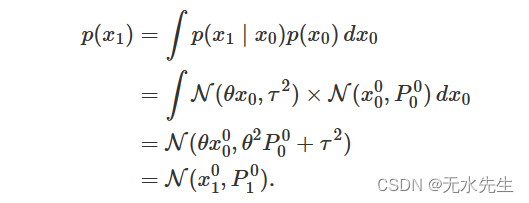
请注意，我们已经定义了 $X^0_1 \doteq \theta X^0_0$ ; $P^0_1 \overset { \Delta }{=} \theta ^2 P^0_0 + \tau ^2$ 。我们可以想到 $X^0_1$ 这是我们根据我们对系统的了解而不是任何数据可以做出的最佳预测。鉴于新的观察 $y_1$ 我们想用这些信息来估计 $x_1$ 。为此我们需要条件分布 $p (x_ 1 | y _1)$ ，称为过滤密度。我们可以用贝叶斯法则来解决这个问题：

$p(x_1\mid y_1) \propto p(y_1\mid x_1)p(x_1)$

从观测方程我们知道 $p(y_1\mid x_1)=\mathcal{N}(x_1, \sigma^2)$ 我们刚刚计算了 $p(x_1)$ 在上面。因此，利用正态分布的基本属性，我们有

$p(x_1\mid y_1) \propto p(y_1\mid x_1)p(x_1)\\ = \varphi(y_1\mid x_1, \sigma^2)\times\varphi(x_1\mid x_1^0, P_1^0)\\ = \mathcal{N}(x_1^0+K_1(y_1-x_1^0), (1-K_1)P_1^0)$

这里：

$K_1 = \frac{P_1^0}{P_1^0 + \sigma^2},$

是卡尔曼增益系数。那么对于 t = 1 我们有了新的估计

$x_1^1 = \mathbb{E}[x_1\mid y_1]\\ = x_1^0+K_1(y_1-x_1^0)$

和

$P_1^1 = \text{Var}(x_1\mid y_1)\\ = (1-K_1)P_1^0.$

所以过滤密度为 $p(x_1\mid y_1) = \mathcal{N}(x_1^1, P_1^1)$

现在让我们迭代一下这个过程 t = 2 我们现在将有一个新的观察结果 $y_2$ 。我们想要计算新的过滤器密度 $X_2$

$p(x_2\mid y_1, y_2) \propto p(y_2\mid x_2)p(x_2\mid y_1).$

上面的陈述隐含的是 $y_2$ 不依赖于 $y_1$ 以价值为条件 $X_2$ 。新的过滤密度 $p(x_2\mid y_1, y_2)$ 是观测数据历史的函数，是观测密度的乘积 $p(y_2\mid x_2)$ 和预测密度 $p(x_2\mid y_1)$ 。在这种情况下，观测密度就是 $\mathcal{N}(x_2, \sigma^2)$ 。预测密度可以通过增加 $p(x_2\mid y_1)$ 与之前的状态值 $x_1$

$p(x_2\mid y_1) = \int p(x_2, x_1\mid y_1)\,dx_1\\ \propto \int p(x_2\mid x_1)p(x_1\mid y_1)\,dx_1.$

在积分内部，我们有状态方程密度和滤波器密度的乘积 $x_1\mid y_1$ ，我们刚刚计算出 $t = 1$ 。状态方程密度为 $\mathcal{N}(\theta x_1, \tau^2)$ 过滤密度为 $\mathcal{N}(x_1^1, P_1^1)$ 。将这些积分出来，我们得到

$p(x_2\mid y_1) \propto \int\varphi(x_2\mid \theta x_1, \tau^2)\varphi(x_1\mid x_1^1, P_1^1)\,dx_1\\ = \varphi(x_2\mid \theta x_1^1, \theta^2 P_1^1 + \tau^2)\\ = \varphi(x_2\mid x_2^1, P_2^1)$

将我们刚刚计算的预测密度与观测密度相结合，我们得到

$p(x_2\mid y_1, y_2) \propto \varphi(y_2\mid x_2,\sigma^2)\varphi(x_2\mid x_2^1, P_2^1)\\ = \mathcal{N}(x_2^1 + K_2(y_2-x_2^1),\, (1-K_2)P_2^1)$

这里：

$K_2 = \frac{P_2^1}{P_2^1 + \sigma^2}$

是新的卡尔曼增益系数。如果我们定义 $x_2^2=x_2^1 + K_2(y_2-x_2^1)$ 和 $P_2^2=(1-K_2)P_2^1$ 那么我们就有了 $p(x_2\mid y_1,y_2)=\mathcal{N}(x_2^2, P_2^2)$ 。我们怎么办 $t = 3$ 只是为了好玩？给出一个新的观察结果 $y_ 3$ ，我们想要新的过滤器密度

$p(x_3\mid y_1, y_2, y_3) \propto p(y_3\mid x_3) p(x_3\mid y_1, y_2).$

使用与之前相同的想法，我们知道观察密度 $p(y_3\mid x_3)$ 预测密度为

$p(x_3\mid y_1, y_2) = \int p(x_3, x_2\mid y_1, y_2)\,dx_2\\ \propto \int p(x_3\mid x_2)p(x_2\mid y_1, y_2)\,dx_2\\ = \int \varphi(x_3\mid \theta x_2, \tau^2)\varphi(x_2\mid x_2^2, P_2^2)\,dx_2\\ = \varphi(x_3\mid \theta x_2^2,\, \theta^2P_2^2+\tau^2)\\ = \varphi(x_3\mid x_3^2, P_3^2)$

现在新的过滤器密度是

$p(x_3\mid y_1, y_2, y_3) \propto p(y_3\mid x_3) p(x_3\mid y_1, y_2)\\ = \varphi(y_3\mid x_3, \sigma^2)\varphi(x_3\mid x_3^2, P_3^2)\\ = \mathcal{N}(x_3^2 + K_3(y_3-x_3^2),\,(1-K_3)P_3^2)$