网站建设需要资质么广州推广排名
文章目录
- 一、二叉树定义、分类
- 二、二叉树的存储结构
- 三、创建二叉树
- 四、遍历方式
一、二叉树定义、分类
- 二叉树:是N个结点的有序集合,该集合或者为空集,或者由一个根节点跟两棵互不相交的、分别称为根节点的左子树或者右子树的二叉树组成。每个结点最多有两个子树。左子树跟右子树是有序的。
- 满二叉树:二叉树深度为k (k≥1)时,第k层有2^(k-1)个节点,二叉树总共有 。
- 完全二叉树:只有最下面两层有度数小于2的节点,且最下面一层的叶节点集中在最左边的若干位置上。具有n个节点的完全二叉树的深度为: (log2n)+1 或 log2(n+1)
二叉树的特点:
- 在k层中的最大节点个数为 2^(k-1);
- 层数为k的树的最大节点个数为 2^k - 1;
- 叶节点的个数比度数为2的节点的个数要多1个: n0 = n2+1
- 总节点数为各类节点之和:n=no+n1+n2
- 总节点数为所有子节点数加一: n= n + 2*n2+ 1 故得: no=n2+1
二、二叉树的存储结构
以二叉链表存储为例
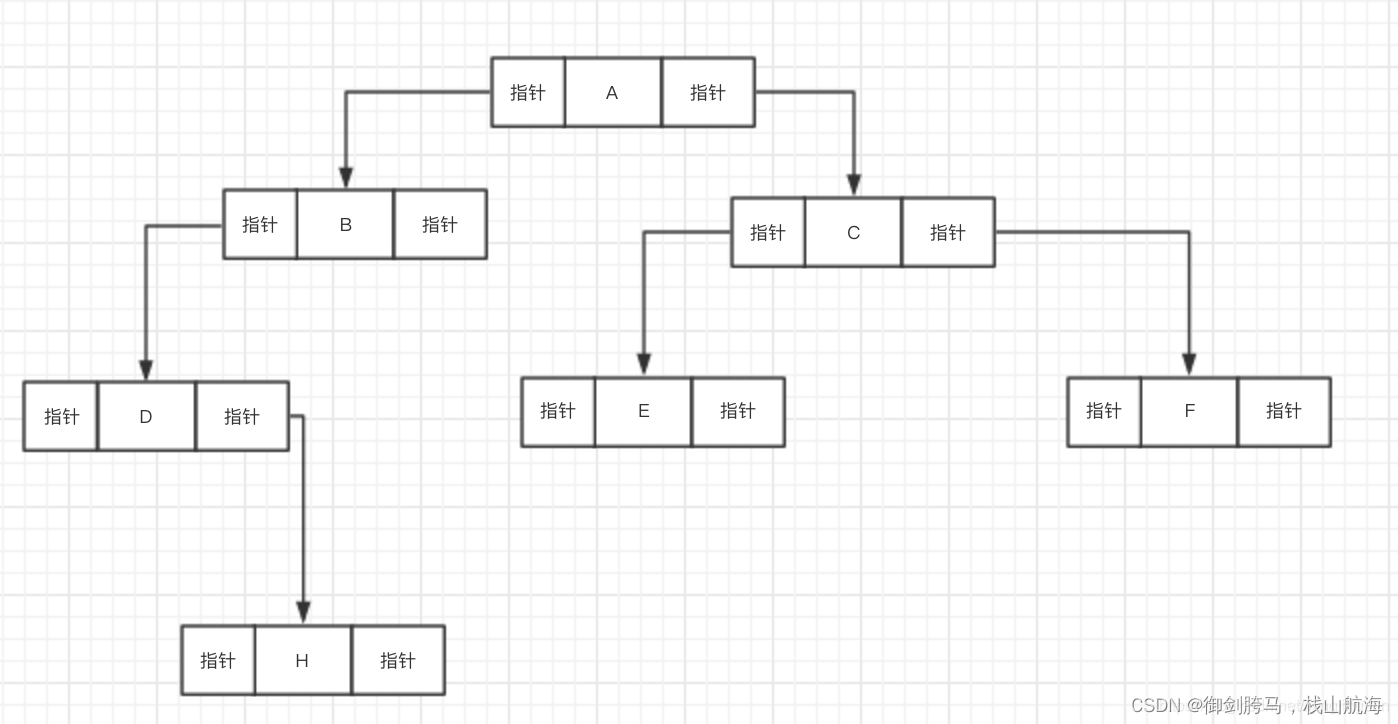
结构:
public class BinaryNode {//左节点public BinaryNode left;//数据域public int data;//右节点public BinaryNode right;public BinaryNode() {}public BinaryNode(int data) {this.data = data;}
}
三、创建二叉树
思路:相当于插入一系列值到空二叉树中,插入规则为
- 当前值如果小于当下节点值:left非空则直接把值放入left,否则把left当成当下节点 继续递归。
- 当前值如果大于当下节点值:right非空则直接把值放入right,否则把right当成当下节点 继续递归。
public class BinaryTree<V> {//根节点,默认为nullprivate BinaryNode root = null;/*** 描述: 构建二叉树* Node:节点,* data:待插入的数据*/private void buildBinaryTree(BinaryNode node, int data) {if (root == null) {root = new BinaryNode(data);return;}//根节点不为空,那么判断数据是否小于当前节点的数据if (data < node.data) {//如果小于,判断当前节点是否有左叶子节点if (node.left == null) {//左叶子节点为空,设置左叶子节点,并且设置数据node.left = new BinaryNode(data);} else {//左叶子节点不为空,递归调用构建二叉树的函数this.buildBinaryTree(node.left, data);}} else {//如果大于或等于,判断当前节点是否存在右叶子节点if (node.right == null) {//右叶子节点为空,设置右叶子节点,并且设置数据域node.right = new BinaryNode(data);} else {//右叶子节点点不为空,递归调用构建二叉树的函数this.buildBinaryTree(node.right, data);}}}/*** 前序遍历*/public void preOrder(BinaryNode node) {System.out.println(node.data);if (node.left != null) {this.midOrder(node.left);}if (node.right != null) {this.midOrder(node.right);}}/*** 中序遍历* */public void midOrder(BinaryNode node) {if (node.left != null) {this.midOrder(node.left);}System.out.println(node.data);if (node.right != null) {this.midOrder(node.right);}}/*** 后序遍历*/public void afterOrder(BinaryNode node) {if (node.left != null) {this.midOrder(node.left);}if (node.right != null) {this.midOrder(node.right);}System.out.println(node.data);}public static BinaryTree createBinaryTree(int[] datas) {BinaryTree binaryTree = new BinaryTree();for (int data : datas) {binaryTree.buildBinaryTree(binaryTree.root, data);}return binaryTree;}/*** 描述: 创建二叉树函数* int[] 是个int类型的数组* 通过循环调用,往二叉树插入数据*/public static void main(String[] arg) {int[] datas = new int[]{1, 9, 8, 2, 10};//构建二叉树BinaryTree binaryTree = createBinaryTree(datas);//前序遍历System.out.println("前序遍历");binaryTree.preOrder(binaryTree.root);//中序遍历System.out.println("中序遍历");binaryTree.midOrder(binaryTree.root);//后续遍历System.out.println("后序遍历");binaryTree.afterOrder(binaryTree.root);}
}
四、遍历方式
总结:通过看父节点的输出先后顺序,就可以判断是什么遍历方式。
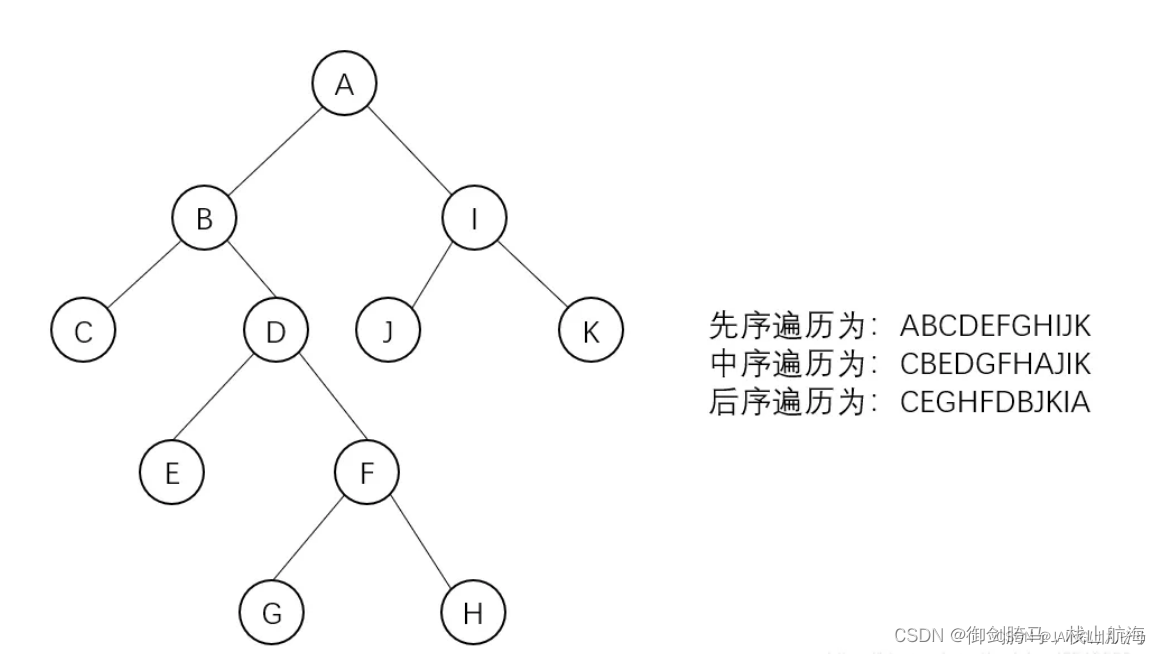
分为三种遍历:
- 前序遍历:先输出父节点, 再遍历左子树和右子树。
- 中序遍历:先遍历左子树, 再输出父节点, 再遍历右子树。
- 后序遍历:先遍历左子树, 再遍历右子树, 最后输出父节点。