年收入100万要交多少税镇江搜索优化技巧

数组、链表和树存储方式分析

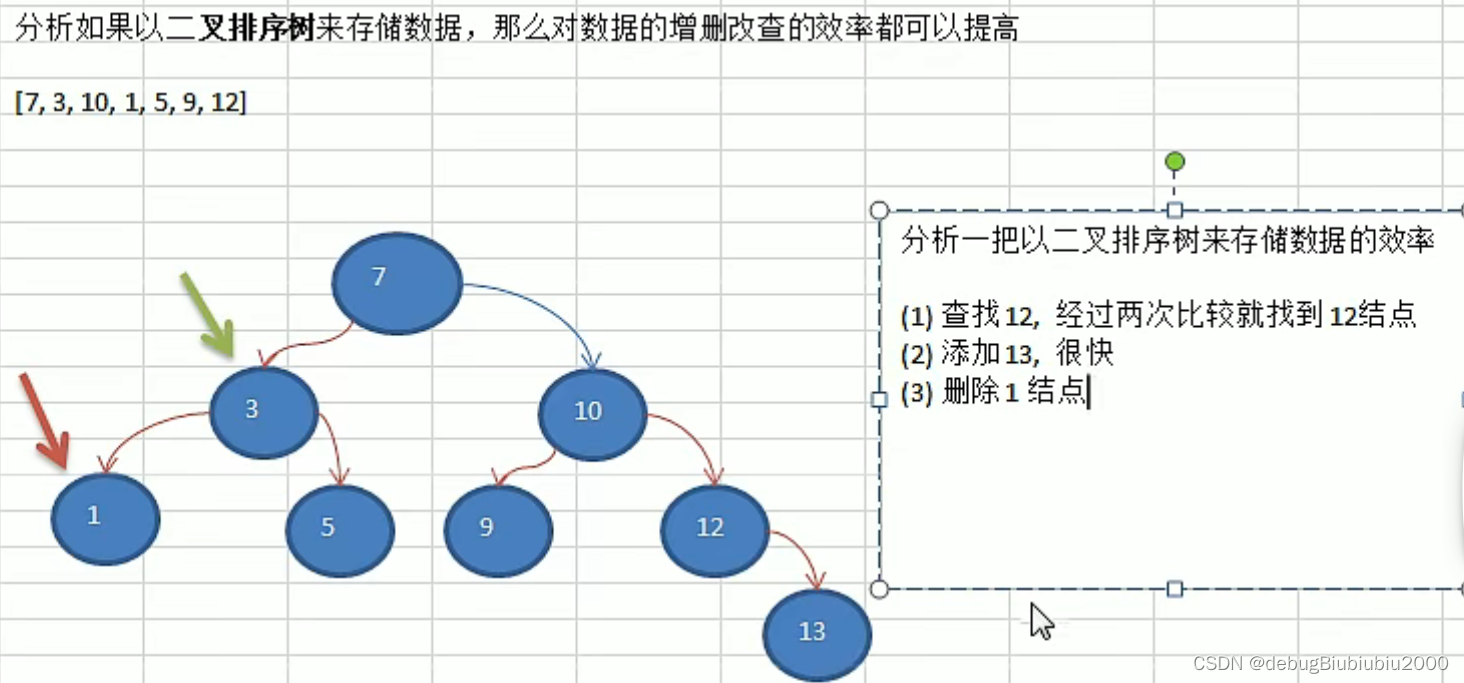
对于树结构，不论是查找修改还是增加删除，效率都比较高，结合了链表和数组的优点，如以下的二叉树：

1、数组的第一个元素作为第一个节点

2、数组的第二个元素3比7小，放在7的左边

3、数组的第三个元素10比7大，放在7的右边

4、数组的第四个元素1比7小，也比3小，放在3的左边

5、数组的第五个元素5比7小，但比3大，放在3的右边

6、数组的第六个元素9比7大，但比10小，放在10的左边

7、数组的第七个元素12比7大，比10大，放在10的右边

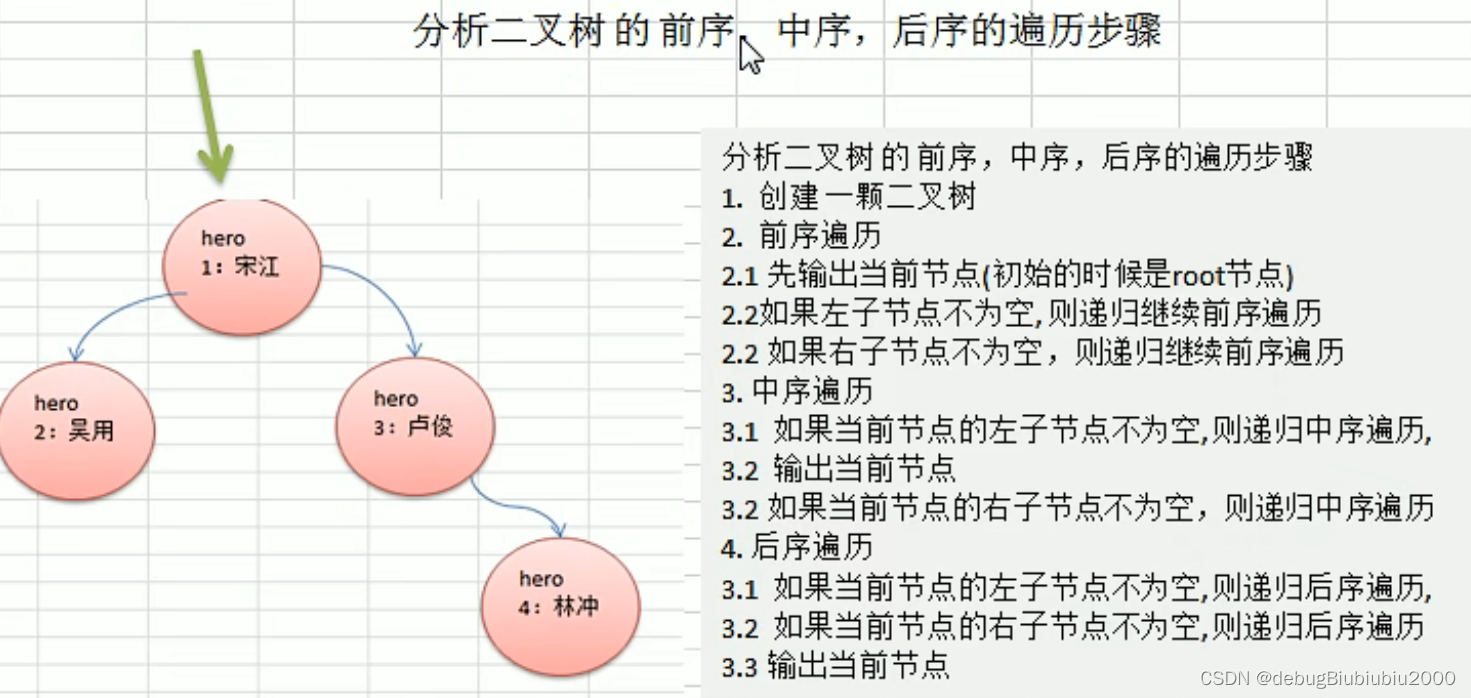
二叉树的前中后序遍历

思路分析

代码实现

# 创建 HeroNode 节点
class HeroNode:def __init__(self, no: int, name: str):self.no = noself.name = nameself.left = Noneself.right = Nonedef __str__(self):return f"no={self.no}, name={self.name}"# 前序遍历def pre_order(self):# 先输出父节点print(self, end=' => ')# 左子树不为空则递归左子树if self.left is not None:self.left.pre_order()# 右子树不为空则递归右子树if self.right is not None:self.right.pre_order()# 中序遍历def infix_order(self):# 左子树不为空则递归左子树if self.left is not None:self.left.infix_order()# 输出父节点print(self, end=' => ')# 右子树不为空则递归右子树if self.right is not None:self.right.infix_order()# 后序遍历def post_order(self):# 左子树不为空则递归左子树if self.left is not None:self.left.post_order()# 右子树不为空则递归右子树if self.right is not None:self.right.post_order()# 输出父节点print(self, end=' => ')# 建立 HeroNode 二叉树
class BinaryTree:root: HeroNode = None# 前序遍历def pre_order(self):if self.root is not None:self.root.pre_order()else:print("二叉树为空...")# 前序遍历def infix_order(self):if self.root is not None:self.root.infix_order()else:print("二叉树为空...")# 前序遍历def post_order(self):if self.root is not None:self.root.post_order()else:print("二叉树为空...")def test_binary_tree():# 手动创建二叉树binary_tree = BinaryTree()root = HeroNode(1, '宋江')node2 = HeroNode(2, '吴用')node3 = HeroNode(3, '卢俊义')node4 = HeroNode(4, '林冲')root.left = node2root.right = node3node3.right = node4binary_tree.root = root# 前序print("前序遍历：", end=" ")binary_tree.pre_order()print()# 中序print("中序遍历：", end=" ")binary_tree.infix_order()print()# 后序print("后序遍历：", end=" ")binary_tree.post_order()print()test_binary_tree()

二叉树的前中后序查找

思路分析

代码实现

""" 前中后序遍历查找 """
# 创建 HeroNode 节点
class HeroNode:def __init__(self, no: int, name: str):self.no = noself.name = nameself.left = Noneself.right = Nonedef __str__(self):return f"no={self.no}, name={self.name}"# 前序遍历查找def pre_order_search(self, no: int):"""前序遍历查找某个节点:param no: 要查找节点的 id:return: 找到的 HeroNode 节点或 None"""print("进入前序遍历...")if self.no == no:  # 如果当前节点是，直接返回return selffind_node = None# 如果左子节点不为空，则向左子节点继续递归查找# 找到则返回，找不到则看右子节点if self.left is not None:find_node = self.left.pre_order_search(no)if find_node:  # 说明在左子树上找到，直接返回return find_node# 否则判断右子节点，若不为空，向右子树递归查找if self.right is not None:find_node = self.right.pre_order_search(no)# 如果右子树找到，则find_node有值，否则find_node为空return find_node# 中序遍历查找def infix_order_search(self, no: int):"""中序遍历查找某个节点:param no: 要查找节点的 id:return: 找到的 HeroNode 节点或 None"""find_node = None# 如果左子节点不为空，则向左子节点继续递归查找# 找到则返回，找不到则看右子节点if self.left is not None:find_node = self.left.infix_order_search(no)if find_node:  # 说明在左子树上找到，直接返回return find_nodeprint("进入中序遍历...")if self.no == no:  # 如果当前节点是，直接返回return self# 否则判断右子节点，若不为空，向右子树递归查找if self.right is not None:find_node = self.right.infix_order_search(no)# 如果右子树找到，则find_node有值，否则find_node为空return find_node# 后序遍历查找def post_order_search(self, no: int):"""后序遍历查找某个节点:param no: 要查找节点的 id:return: 找到的 HeroNode 节点或 None"""find_node = None# 如果左子节点不为空，则向左子节点继续递归查找# 找到则返回，找不到则看右子节点if self.left is not None:find_node = self.left.post_order_search(no)if find_node:  # 说明在左子树上找到，直接返回return find_node# 否则判断右子节点，若不为空，向右子树递归查找if self.right is not None:find_node = self.right.post_order_search(no)# 如果右子树找到，则find_node有值，否则find_node为空if find_node:return find_nodeprint("进入后序遍历...")if self.no == no:  # 如果当前节点是，直接返回return selfreturn None# 建立 HeroNode 二叉树
class BinaryTree:root: HeroNode = None# 前序查找def pre_order_search(self, no):if self.root is not None:return self.root.pre_order_search(no)else:return None# 中序查找def infix_order_search(self, no):if self.root is not None:return self.root.infix_order_search(no)else:return None# 后序查找def post_order_search(self, no):if self.root is not None:return self.root.post_order_search(no)else:return Nonedef test_binary_tree():# 手动创建二叉树binary_tree = BinaryTree()root = HeroNode(1, '宋江')node2 = HeroNode(2, '吴用')node3 = HeroNode(3, '卢俊义')node4 = HeroNode(4, '林冲')node5 = HeroNode(5, "关胜")root.left = node2root.right = node3node3.right = node4node3.left = node5binary_tree.root = rootprint("前序遍历查找：")  # 比较了4次（看输出得到的结果）res = binary_tree.pre_order_search(5)if res:print("找到了，节点信息为：", res)else:print("找不到编号为5的节点")print()print("中序遍历查找：")  # 比较了3次（看输出得到的结果）res = binary_tree.infix_order_search(5)if res:print("找到了，节点信息为：", res)else:print("找不到编号为5的节点")print()print("后序遍历查找：")  # 比较了2次（看输出得到的结果）res = binary_tree.post_order_search(5)if res:print("找到了，节点信息为：", res)else:print("找不到编号为5的节点")test_binary_tree()

二叉树删除节点

思路分析

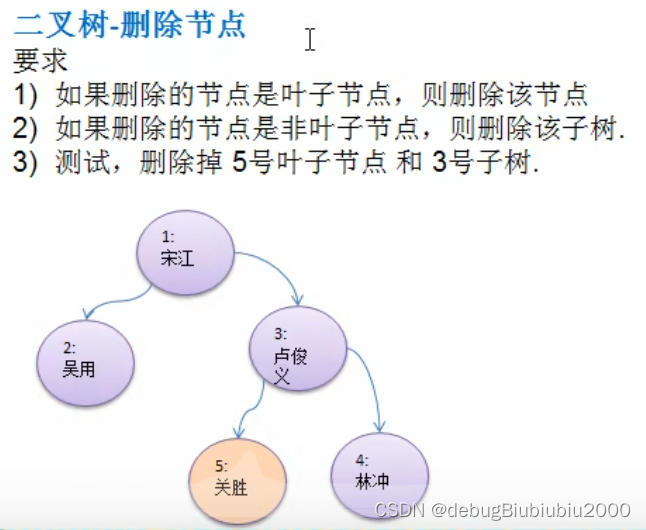
代码实现

""" 递归删除二叉树节点 """
# HeroNode 节点
class HeroNode:def __init__(self, no: int, name: str):self.no = noself.name = nameself.left = Noneself.right = Nonedef __str__(self):return f"no={self.no}, name={self.name}"# 前序遍历def pre_order(self):# 先输出父节点print(self, end=' => ')# 左子树不为空则递归左子树if self.left is not None:self.left.pre_order()# 右子树不为空则递归右子树if self.right is not None:self.right.pre_order()def delete_node(self, no: int):"""递归删除节点规则：如果删除的节点是叶子节点，则直接删除如果删除的节点不是叶子节点，则删除该节点及其左右子树:param no: 要删除的节点编号:return:"""# 如果左子节点不为空，且左子节点是要删除的节点，则删除左子节点及其子树，并返回if self.left and self.left.no == no:self.left = None  # 相当于删除左子节点及其子树return# 如果右子节点不为空，且右子节点是要删除的节点，则删除右子节点及其子树，并返回if self.right and self.right.no == no:self.right = None  # 相当于删除右子节点及其子树return# 如果左右子节点都不是要删除的节点，则首先向左子节点递归删除if self.left:self.left.delete_node(no)# 如果递归完左子节点还没找到要删除的节点，则继续向右子节点递归删除if self.right:self.right.delete_node(no)# 建立 HeroNode 二叉树
class BinaryTree:root: HeroNode = None# 前序遍历def pre_order(self):if self.root is not None:self.root.pre_order()else:print("二叉树为空...")# 删除树节点def delete_node(self, no: int):if self.root:if self.root.no == no:  # 如果根节点是要删除的节点self.root = None  # 则把根节点置空else:self.root.delete_node(no)else:print("树空，不能删除节点...")def test_binary_tree():# 手动创建二叉树binary_tree = BinaryTree()root = HeroNode(1, '宋江')node2 = HeroNode(2, '吴用')node3 = HeroNode(3, '卢俊义')node4 = HeroNode(4, '林冲')node5 = HeroNode(5, "关胜")root.left = node2root.right = node3node3.right = node4node3.left = node5binary_tree.root = rootprint("删除前：", end='')binary_tree.pre_order()print()binary_tree.delete_node(5)print("删除后：", end='')binary_tree.pre_order()print()test_binary_tree()

顺序存储二叉树

思路分析

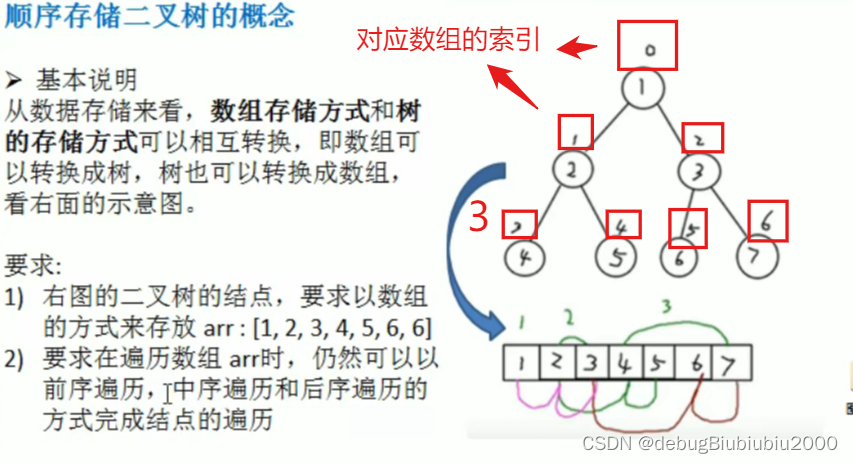
代码实现

需求如下：

"""顺序存储二叉树"""
# 顺序存储二叉树就是用数组结构存储二叉树节点数据，
# 要求用数组存储后，可以对该数组进行前序遍历、中序遍历、后序遍历
# 其实就是将二叉树从左到右，从上到下的节点依次存入数组中，如下：
"""
假设有如下一棵二叉树，它对应的顺序存储就是：arr = [1, 2, 3, 4, 5, 6, 7]12      34    5  6    7
"""
class ArrayBinaryTree:def __init__(self, arr):self.arr = arrdef pre_order(self, index: int):"""以前序遍历方式访问数组元素:param index: 数组下标:return:"""n = len(self.arr)  # n为数组长度if self.arr and n > 0:# 输出当前元素print(f"arr[{index}]={self.arr[index]}", end=" ")# 向左子树递归if 2 * index + 1 < n:self.pre_order(2 * index + 1)# 向右子树递归if 2 * index + 2 < n:self.pre_order(2 * index + 2)else:print("数组为空！")def infix_order(self, index: int):"""以中序遍历方式访问数组元素:param index: 数组下标:return:"""n = len(self.arr)if self.arr and n > 0:if 2 * index + 1 < n:  # 向左子树递归self.infix_order(2 * index + 1)print(f"arr[{index}]={self.arr[index]}", end=" ")if 2 * index + 2 < n:  # 向右子树递归self.infix_order(2 * index + 2)else:print("数组为空")def post_order(self, index: int):"""以后序遍历方式访问数组元素:param index: 数组下标:return:"""n = len(self.arr)if self.arr and n > 0:if 2 * index + 1 < n:  # 向左子树递归self.post_order(2 * index + 1)if 2 * index + 2 < n:  # 向右子树递归self.post_order(2 * index + 2)print(f"arr[{index}]={self.arr[index]}", end=" ")arr_binary_tree = ArrayBinaryTree([1, 2, 3, 4, 5, 6, 7])
print("前序遍历：")
arr_binary_tree.pre_order(0)
print()
print("中序遍历：")
arr_binary_tree.infix_order(0)
print()
print("后序遍历：")
arr_binary_tree.post_order(0)
print()

线索化二叉树

简单介绍

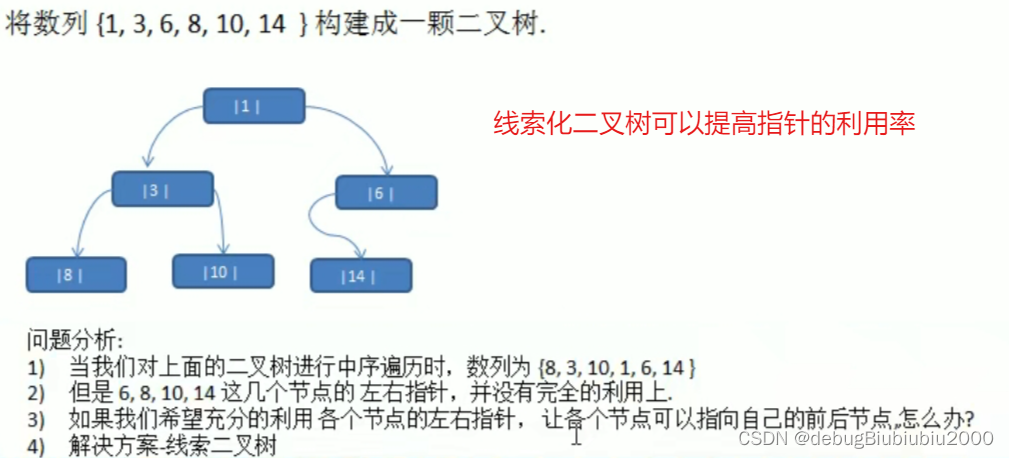
思路分析

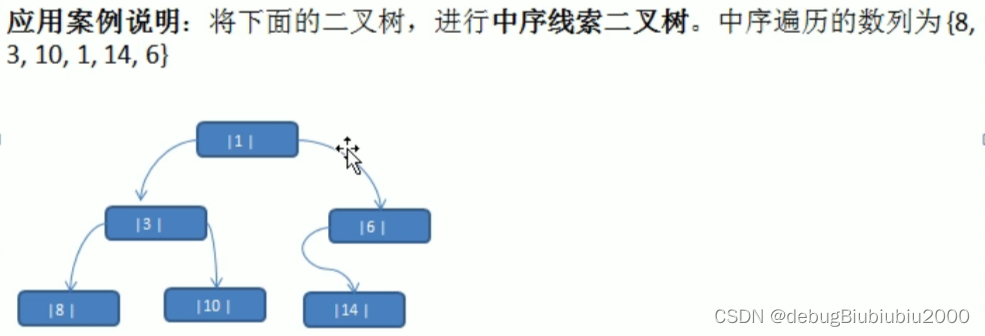
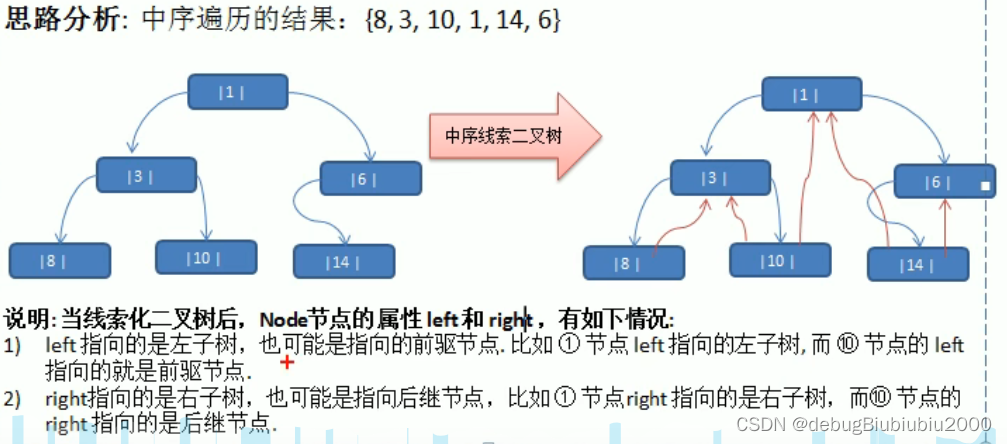
遍历线索化二叉树

线索化二叉树和遍历线索化二叉树的代码实现

""" 线索化二叉树 """
# 创建 Node 节点
class Node:no: int = Noneleft = Noneright = None# left_type/right_type 表示指针类型# 值为0时表示指向的是左子树/右子树，为1时表示指向的是前驱节点/后继节点left_type: int = 0right_type: int = 0def __init__(self, no: int):self.no = noself.left = Noneself.right = Nonedef __str__(self):return f"no={self.no}"# 建立线索化 Node 二叉树
class ThreadedBinaryTree:root: Node = None# 为了实现线索化，需要一个指针（变量）指向当前节点的前驱节点# 如中序线索化中，需要一个指针（变量）指向当前节点在中序遍历结果中的前驱节点# 在递归进行线索化时， pre 总指向当前节点按某种遍历方式结果的前驱节点pre: Node = None# 建立中序线索化二叉树def threaded_infix_tree(self, node: Node):"""建立中序线索化二叉树:param node: 要线索化的节点:return:"""if node is None:  # 节点为空，不需要线索化return# 先线索化左子树self.threaded_infix_tree(node.left)# 线索化当前节点# 结合图形理解代码，第一个要线索化的节点是8# 先处理当前节点的左子节点if node.left is None:  # 如果当前节点的左指针为空，则让左指针指向当前节点的前驱节点prenode.left = self.prenode.left_type = 1  # 设置指针类型为1，表示该指针指向的是前驱节点# 处理后继节点if self.pre and  self.pre.right is None:self.pre.right = nodeself.pre.right_type = 1  # 设置指针类型为1，表示该指针指向的是后继节点# 每处理一个节点后，让当前节点成为下一个节点的前驱节点self.pre = node# 后线索化右子树self.threaded_infix_tree(node.right)# 遍历中序线索化二叉树def for_in_tree(self):node = self.rootwhile node:# 循环找到 left_type = 1 的节点，该节点就是中序遍历的第一个节点，即图中的节点8while node.left_type == 0:node = node.left# 输出当前节点print(node, end=" ")# 如果当前节点的右指针指向的是后继节点，则一直输出while node.right_type == 1:node = node.rightprint(node, end=" ")# 替换要遍历的节点，具体过程通过debug和结合图来看会更容易理解node = node.rightdef test_binary_tree():# 手动创建二叉树binary_tree = BinaryTree()root = Node(1)node2 = Node(3)node3 = Node(6)node4 = Node(8)node5 = Node(10)node6 = Node(14)root.left = node2root.right = node3node2.left = node4node2.right = node5node3.left = node6threaded_binary_tree = ThreadedBinaryTree()threaded_binary_tree.root = root# 测试线索化print(f"线索化前：10的left={node5.left}，right={node5.right}")threaded_binary_tree.threaded_infix_tree(root)# 以10号节点，即node5测试print(f"线索化后：10的前驱节点={node5.left}，后继节点={node5.right}")# 测试遍历线索化二叉树threaded_binary_tree.for_in_tree()test_binary_tree()