访问国外网站的软件wordpress官网入口

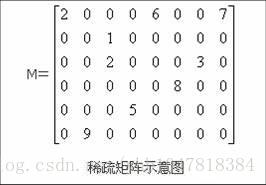
稀疏矩阵：

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。

特性：
1.稀疏矩阵其非零元素的个数远远小于零元素的个数，而且这些非零元素的分布也没有规律。
2.稀疏因子是用于描述稀疏矩阵的非零元素的比例情况。设一个n*m的稀疏矩阵A中有t个非零元素，则稀疏因子δδ的计算公式如下：δ=tn∗mδ=tn∗m(当这个值小于等于0.05时，可以认为是稀疏矩阵)

矩阵压缩：

存储矩阵的一般方法是采用二维数组，其优点是可以随机地访问每一个元素，因而能够较容易地实现矩阵的各种运算，如转置运算、加法运算、乘法运算等。
对于稀疏矩阵来说，采用二维数组的存储方法既浪费大量的存储单元用来存放零元素，又要在运算中花费大量的时间来进行零元素的无效计算。所以必须考虑对稀疏矩阵进行压缩存储。

最常用的稀疏矩阵存储格式主要有：COO（Coordinate Format）和CSR（Compressed Sparse Row）。

COO很简单，就是使用3个数组，分别存储全部非零元的行下标（row index）、列下标（column index）和值（value）；CSR稍复杂，对行下标进行了压缩，假设矩阵行数是m，则压缩后的数组长度为m+1，记作（row ptr），其中第i个元素（0-base）表示矩阵前i行的非零元个数。

（1）Coordinate（COO）

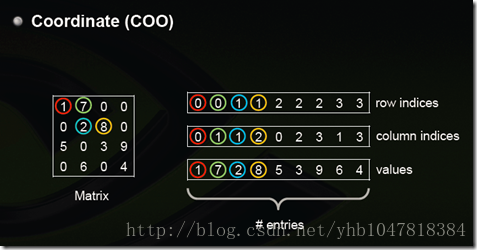
这是最简单的一种格式，每一个元素需要用一个三元组来表示，分别是（行号，列号，数值），对应上图右边的一列。这种方式简单，但是记录单信息多（行列），每个三元组自己可以定位，因此空间不是最优。

（2）Compressed Sparse Row (CSR)

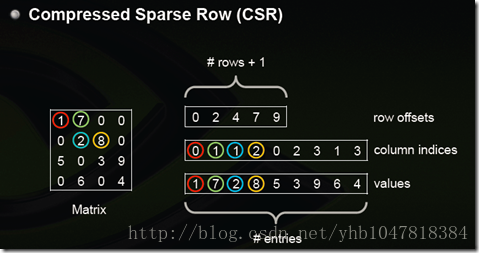
CSR是比较标准的一种，也需要三类数据来表达：数值，列号，以及行偏移。CSR不是三元组，而是整体的编码方式。数值和列号与COO一致，表示一个元素以及其列号，行偏移表示某一行的第一个元素在values里面的起始偏移位置。如上图中，第一行元素1是0偏移，第二行元素2是2偏移，第三行元素5是4偏移，第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数，本例中是9。

CSC是和CSR相对应的一种方式，即按列压缩的意思。
以上图中矩阵为例：
Values： [1 5 7 2 6 8 3 9 4]
Row Indices：[0 2 0 1 3 1 2 2 3]
Column Offsets：[0 2 4 7 9]

其他的存储格式如：CSC,DIA,ELL,HYB等参考博文
http://blog.csdn.net/gggg_ggg/article/details/47402459

稀疏矩阵的实现：

/** @describe: sparse matrix* @date: 2018/02/28*/#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include "SparseMatrix.h"
#include "common.h"
#include "MyTime.h"//coo转化为csr矩阵
void coo_to_csr_sparse_matrix(COOSparseMatrix *cm, CSRSparseMatrix *sm)
{unsigned int i, j;unsigned int tot = 0;int nz, nr;nz = cm->NonZeroNum;nr = cm->rowNum + 1;// Init mem for CSR matrixsm->val = (double *)malloc(nz * sizeof(double));sm->col = (unsigned int *)malloc(nz * sizeof(unsigned int));sm->ptr = (unsigned int *)malloc(nr * sizeof(unsigned int));memset(sm->ptr, 0, nr * sizeof(unsigned int));sm->NonZeroNum = cm->NonZeroNum;sm->rowNum = cm->rowNum;sm->colNum = cm->colNum;sm->ptr[0] = tot;for (i = 0; i < sm->rowNum; i++){for (j = 0; j < cm->NonZeroNum; j++){if (cm->row[j] == i){sm->val[tot] = cm->val[j];sm->col[tot] = cm->col[j];tot++;sm->ptr[i + 1] = tot;}}}}//创建coo矩阵
void create_coo_sparse_matrix(COOSparseMatrix *cm)
{int i,nz;int m, n;double t;FILE *fp;nz = cm->NonZeroNum;printf("len:%d\n", nz);cm->val = (double *)malloc(nz * sizeof(double));cm->row = (unsigned int *)malloc(nz * sizeof(unsigned int));cm->col = (unsigned int *)malloc(nz * sizeof(unsigned int));m = n = 0;t = 0.0;fp = fopen(FILE_PATH, "r");if (fp == NULL){printf("file does not exist");return;}for (i = 0; i < nz; i++){fscanf(fp, "%d %d %lf\n", &m, &n, &t);//printf("row:%d, col:%d, val:%lf\n", m, n, t);cm->row[i] = m;cm->col[i] = n;cm->val[i] = t;}fclose(fp);
}//删除矩阵
void free_csr_sparse_matrix(CSRSparseMatrix *coo)
{       if (coo->col != NULL)free(coo->col);if (coo->ptr != NULL)free(coo->ptr);if (coo->val != NULL)free(coo->val);coo->col = NULL;coo->ptr = NULL;coo->val = NULL;coo->colNum = coo->rowNum = coo->NonZeroNum = 0;
}void free_coo_sparse_matrix(COOSparseMatrix *coo)
{if (coo->row != NULL)free(coo->row);if (coo->col != NULL)free(coo->col);if (coo->val != NULL)free(coo->val);coo->row = NULL;coo->col = NULL;coo->val = NULL;coo->colNum = coo->rowNum = coo->NonZeroNum = 0;}//矩阵加法
int SparseMatrixAdd(CSRSparseMatrix sm1, CSRSparseMatrix sm2, CSRSparseMatrix *output)
{if (sm1.colNum != sm2.colNum || sm1.rowNum != sm2.rowNum)return ERR_FAILED;//to be definedreturn ERR_OK;
}//y = mx
void csr_SPMV(CSRSparseMatrix *csr, double *x, double *y)
{unsigned int i, j, end;double sum;double *val = csr->val;unsigned int *col = csr->col;unsigned int *ptr = csr->ptr;end = 0;// Loop over rows.for (i = 0; i < csr->rowNum; i++){sum = 0.0;j = end;end = ptr[i + 1];// Loop over non-zero elements in row i.for (; j < end; j++){sum += val[j] * x[col[j]];}y[i] = sum;}
}void display_csr_matrix(CSRSparseMatrix *sm)
{unsigned int i,j;printf("val= ");for (i = 0; i < sm->NonZeroNum; i++){printf("%.2g | ", sm->val[i]);}j = 1;printf("\ncol= ");for (i = 0; i < sm->NonZeroNum; i++){printf("%d | ", sm->col[i]);}printf("\nptr= ");for(i=0; i < sm->rowNum + 1; i++){if (sm->ptr[i] != 0 || i==0)printf("%d | ", sm->ptr[i]);}printf("\n");//printf("\tnz= %d\n", m->nz);//printf("\trows= %d\n", m->rows);//printf("\tcols= %d\n", m->cols);
}void create_random_data(int len)
{       int m;int n;double a;int i;FILE *fp;fp = fopen(FILE_PATH, "w+");if (fp == NULL){printf("open file failed!\n");return;}printf("len is %d\n",len);srand((unsigned)time(NULL));for (i = 0; i < len; i++){/*create random data*/m = rand() % 100;n = rand() % 100;a = rand() / (double)(RAND_MAX);fprintf(fp, "%d %d %lf\n", m, n, a);}fclose(fp);
}int main(int argc, char *argv[])
{       double *x;double *y;int m_rows = 100;int m_cols = 100;int n_zeros = 9;int loops = 1000;MyTime mytime;int i;COOSparseMatrix coo;CSRSparseMatrix csr;LINEPRINT;//create_random_data(n_zeros);if (strcmp("create", argv[1]) == 0){printf("now create random data!\n");create_random_data(n_zeros);        }coo.rowNum = m_rows;coo.NonZeroNum = n_zeros;coo.colNum = m_cols;create_coo_sparse_matrix(&coo);coo_to_csr_sparse_matrix(&coo, &csr);display_csr_matrix(&csr);free_coo_sparse_matrix(&coo);x = (double *)malloc(m_cols *sizeof(double));y = (double *)malloc(m_rows *sizeof(double));for (i = 0; i < csr.colNum; i++){x[i] = i + 1;}//计算y = mx的时间time_start(&mytime);for (i = 0; i < loops; i++){csr_SPMV(&csr, x, y);}time_stop(&mytime);printf("smmv use time:%lf\n", mytime.sec);free_csr_sparse_matrix(&csr);free(x);free(y);x = NULL;y = NULL;exit(EXIT_SUCCESS);return 0;}

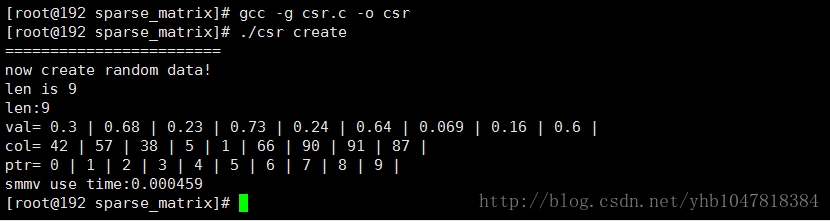
主要实现了coo创建稀疏矩阵，转化为csr稀疏矩阵，以及稀疏矩阵的矢量乘法

结果：

稀疏矩阵的优化：

最近考虑稀疏矩阵的优化，但是看不到MKL的实现，想了几个思路，不知道对稀疏矩阵的优化有没有帮助，暂时先记下来。
1.多线程。使用openmp或者mpi
2.numanode awareness 特性。把稀疏矩阵的存储均匀地分配到两颗处理器各自的本地内存中，最大程度的利用内存带宽
3.利用硬件cache特性，对矩阵进行分块或矩阵的循环进行限制
4.利用pipeline，多流水线并行处理
5.自适应分块存储结构。由于稀疏矩阵的非零元分布不一定均匀，有的分块会非常稀疏，有的则会相对稠密。对于极稀疏的分块（非零元数量远小于行数），如果用和CSR相似的压缩行存储策略，则会浪费空间，所以用COO的方式反而更能节省存储空间，提高访问效率。