注册资金多少有什么区别抚顺seo

无边的奇迹源自简单规则的无限重复 ---- 分形之父Benoit B.Mandelbrot

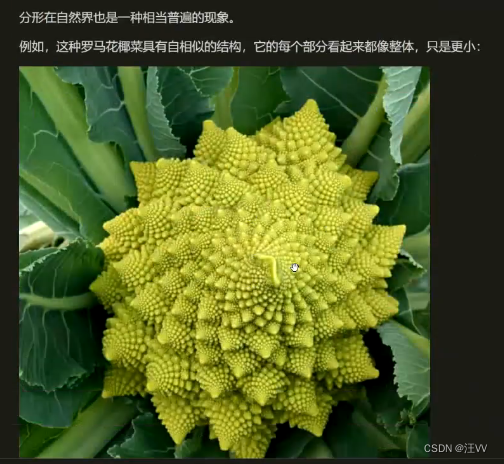
分形的重要特征

• 自相似性
• 无标度性
• 非线性
  

曼德布洛特集合

• $z_0=0$
• $z_{n+1}=z_n^2+c$

想要确定复数c是否属于曼德布洛特集合，只要将c代入上面公式，当n足够大时，如果序列没有发散，则说明c输入曼德布洛特集合。

def iter_m(c):z = cfor i in range(1, 10):z = z**2 + cprint(round(z, 3), end = '->')print('\n' + '*' * 20)
iter_m(-1)
iter_m(-0.5)
iter_m(0.5)# 输出
0->-1->0->-1->0->-1->0->-1->0->
********************
-0.25->-0.438->-0.309->-0.405->-0.336->-0.387->-0.35->-0.377->-0.358->
********************
0.75->1.062->1.629->3.153->10.444->109.567->12005.476->144131442.662->2.0773872763941816e+16->
********************
可以看到-1和0.5不收敛

从图像理解-0.5为什么收敛：
由$z_{n+1}=z_n^2+c$知道$z_1=-0.5$，$z_1$要作下一步的横坐标，因此由$y=x$找到横坐标为$z_1$的点，然后再在曼德布洛特的迭代函数中计算。（win11的计算器绘图不是方格，我稍微查了一下也没找到解决办法，如果有人知道怎么改，希望能留言，感谢）可以看到收敛于交点，至于-1和0.5也可以用同样的方法从图中看出来。

曼德布洛特集合有一个以证明的结论：

复平面上的曼德布洛特集合在一个半径为2的圆内

# 改进后的函数
def iter_m3(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合return Falsez = z**2 + creturn True

图像展示

现提出想要对一个复数区域内的点进行区分是否属于曼德布洛特集合该如何做呢？
先学习两个方法

np.ogrid[]

x, y = np.ogrid[0:1:5j, -1:1:5j] # 前列后行
# 切片第三个参数如果以j结尾则是将其等分划分
# 如果没有j，只是一个数，则是以该数为间隔划分
print('x:\n', x)
print('y:\n', y)
z = x + y * 1j
print('z:\n', z)# 输出
x:[[0.  ][0.25][0.5 ][0.75][1.  ]]
y:[[-1.  -0.5  0.   0.5  1. ]]
z:[[0.  -1.j  0.  -0.5j 0.  +0.j  0.  +0.5j 0.  +1.j ][0.25-1.j  0.25-0.5j 0.25+0.j  0.25+0.5j 0.25+1.j ][0.5 -1.j  0.5 -0.5j 0.5 +0.j  0.5 +0.5j 0.5 +1.j ][0.75-1.j  0.75-0.5j 0.75+0.j  0.75+0.5j 0.75+1.j ][1.  -1.j  1.  -0.5j 1.  +0.j  1.  +0.5j 1.  +1.j ]]

np.frompyfunc()

优点类似于map的功能，但不完全相同。对于上面的iter_m3()方法只能传入一个复数，如果传入一个包含复数的数组则不可以。为了解决这个问题，使用np.frompyfunc(func, nin, nout)
其中func是自定义函数，nin是传入参数的个数，nout是传出参数的个数。

mande = np.frompyfunc(iter_m3, 1, 1)
mande(z)# 输出
array([[True, True, True, True, True],[False, True, True, True, False],[False, False, False, False, False],[False, False, False, False, False],[False, False, False, False, False]], dtype=object)

同样也可以使用map达到该功能，但是复杂一些

result = np.array(list(map(lambda row: list(map(iter_m3, row)), z)))
# 注意：对于二维数组，一层map取的是一维数组
print(result)# 输出
[[ True  True  True  True  True][False  True  True  True False][False False False False False][False False False False False][False False False False False]]

集合转图像

import numpy as np
import matplotlib.pylab as plt
from matplotlib import cmdef iter_m3(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合return Falsez = z**2 + creturn Truedef draw_set(cx, cy, d, ufunc:np.ufunc):x0, x1, y0, y1 = cx - d, cx + d, cy - d, cy + dy, x = np.ogrid[y0:y1:400j, x0:x1:400j]z = x + y * 1jplt.imshow(ufunc(z).astype(float), cmap=cm.jet, extent=[x0, x1, y0, y1])mande = np.frompyfunc(iter_m3, 1, 1)
draw_set(-0.5, 0, 1.5, mande)

输出图像：

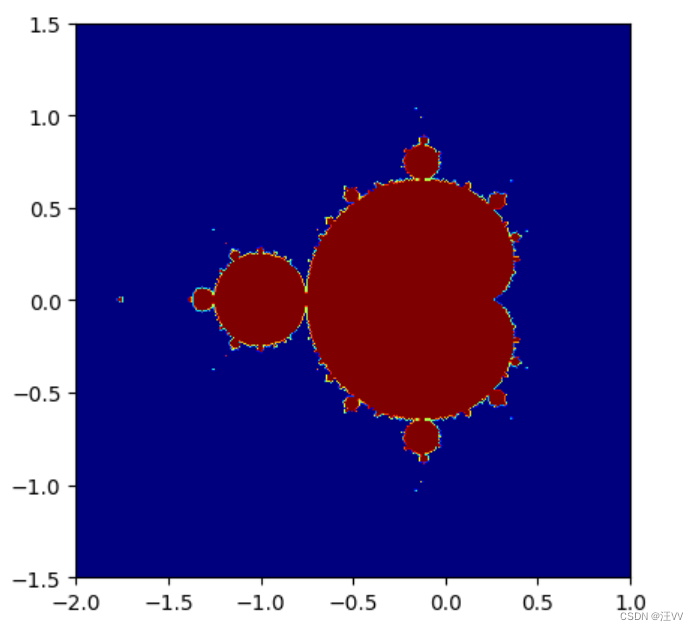
但是颜色不够鲜艳，希望每一个不同的发散点都能显示不同的颜色。

def iter_m4(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合breakz = z**2 + creturn i
mande = np.frompyfunc(iter_m4, 1, 1)
draw_set(-0.5, 0, 1.5, mande)

放大
对（0.273, 0.5921）处进行放大

x, y = 0.273, 0.5921
plt.subplot(2, 3, 1)
draw_set(-0.5, 0, 1.5, mande)
for i in range(2, 7):plt.subplot(2, 3, i)draw_set(x, y, 0.25**(i-1.5), mande)

输出：

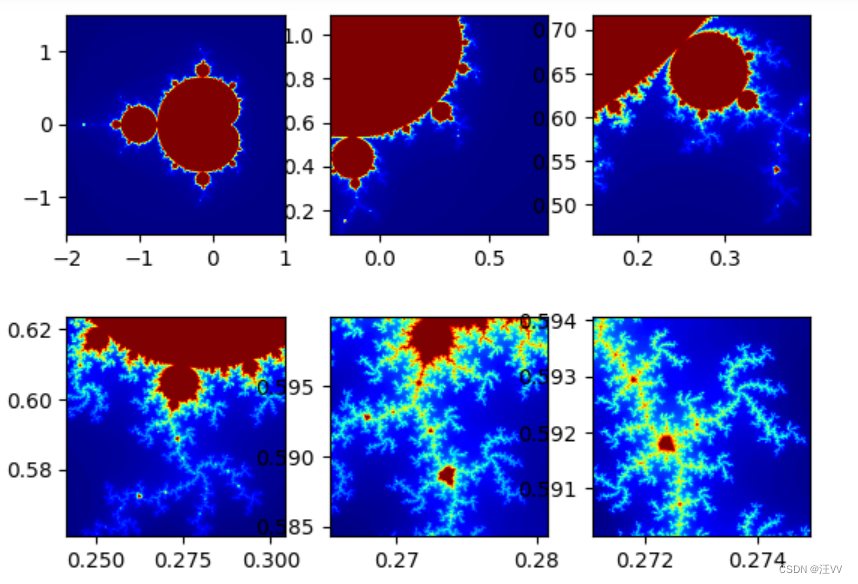
julia集合

迭代公式与曼德布洛特唯一区别在于$z_0$不是0，而是输入数据，c给定一个值，因此曼德布洛特集合只有一个，而julia集合有无数个。

def iter_j(z):c = -0.4 + 0.6jfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合breakz = z**2 + creturn i
julia = np.frompyfunc(iter_j, 1, 1)
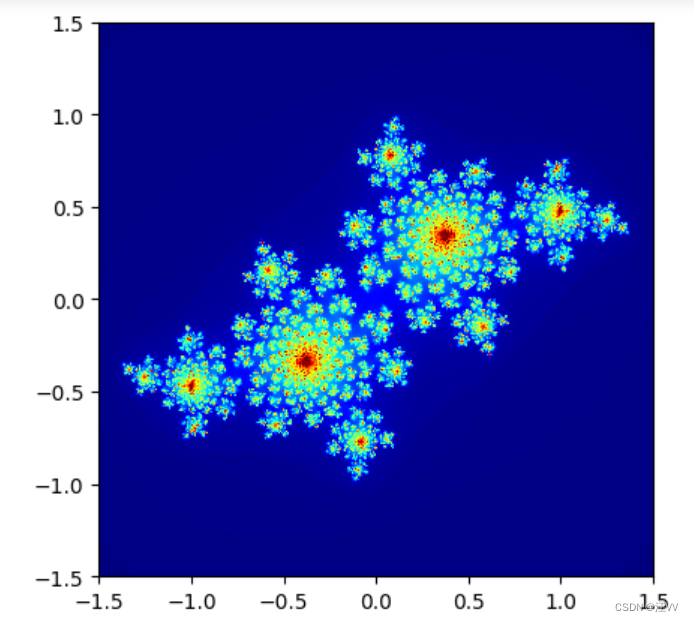
draw_set(0, 0, 1.5, julia)

输出：

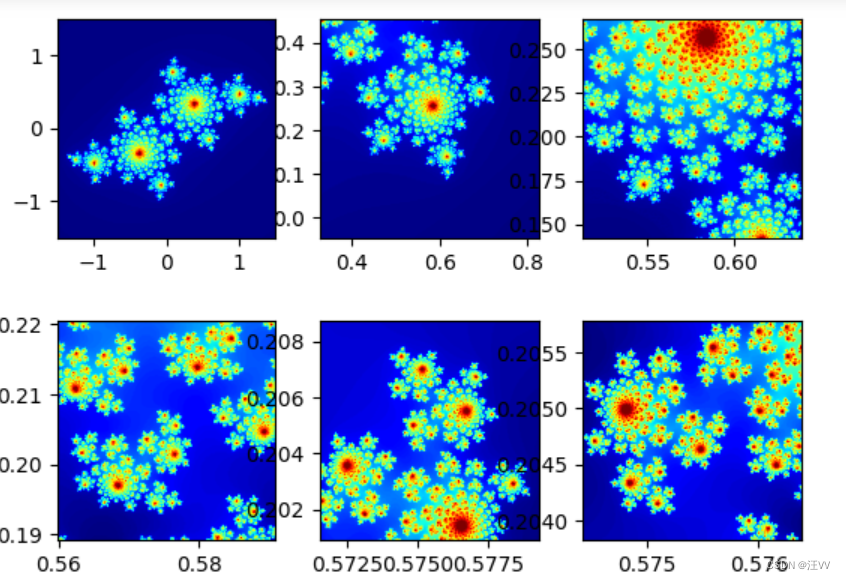
放大

x, y = 0.5754, 0.2048
plt.subplot(2, 3, 1)
draw_set(0, 0, 1.5, julia)
for i in range(2, 7):plt.subplot(2, 3, i)draw_set(x, y, 0.25**(i-1), julia)

输出：